
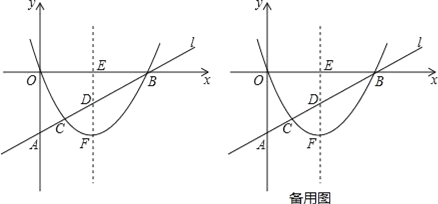
【题目】如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.
(1)设a=![]() ,m=﹣2时,
,m=﹣2时,
①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.
【答案】(1)①(2,﹣1)②(3,﹣ ![]() )(2)y=x2﹣4x
)(2)y=x2﹣4x
【解析】试题分析:(1)①根据待定系数法,可得抛物线的解析式,根据配方法,可得顶点坐标;根据解方程组,可得C点坐标,根据自变量与函数值的对应关系,可得D点坐标;
②根据菱形的性质,可得G点坐标,根据平行四边形的判定,可得答案;
(2)根据待定系数法,可得b与a的关系,根据配方法,可得顶点坐标,根据平行线分线段成比例,可得OH的长,根据自变量与函数值的对应关系,可得C点坐标,根据相似三角形的对应角相等,可得∠FCD=90°,根据相思三角形的性质,可得关于a的方程,根据抛物线的开口向上,可得a的值.
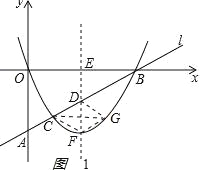
试题解析:(1)①如图1,
 ,
,
当a=![]() 时,将B点坐标代入,得y=
时,将B点坐标代入,得y=![]() x2﹣2x=
x2﹣2x=![]() (x﹣2)2﹣2顶点坐标为(2,﹣2);
(x﹣2)2﹣2顶点坐标为(2,﹣2);
当m=﹣2时,一次函数的解析式为y=![]() x﹣2.
x﹣2.
联立抛物线与直线,得
![]() 2﹣2x=
2﹣2x=![]() x﹣2,
x﹣2,
解得x=1,当x=1时,y=﹣![]() ,即C点坐标为(1,﹣
,即C点坐标为(1,﹣![]() ).
).
当x=2时,y=﹣1,即D点坐标为(2,﹣1);
②假设存在G点,使得以G、C、D、F四点为顶点的四边形是平行四边形.
则CG与DF互相平分,而EF是抛物线的对称轴,且点G在抛物线上
∴CG⊥DF,
∴DCFG是菱形,
∴点C关于EF的对称点G(3,﹣ ![]() ).
).
设DF与CG与DF相交于O′点,则DO′=O′F=![]() ,CO′=O′G=1,
,CO′=O′G=1,
∴四边形DCFG是平行四边形.
∴抛物线y=ax2+bx上存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形,点G的坐标为(3,﹣ ![]() );
);
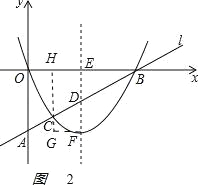
(2)如图2,
 ,
,
∵抛物线y=ax2+bx的图象过(4,0)点,16a+4b=0,
∴b=﹣4a.
∴y=ax2+bx=ax2﹣4ax=a(x﹣2)2﹣4a的对称轴是x=2,
∴F点坐标为(2,﹣4a).
∵三角形FAC的面积与三角形FBC面积之比为1:3,
BC:AC=3:1.
过点C作CH⊥OB于H,过点F作FG∥OB,FG与HC交于G点.
则四边形FGHE是矩形.
由HC∥OA,得BC:AC=3:1.
由HB:OH=3:1,OB=4,OE=EB,得
HE=1,HB=3.
将C点横坐标代入y=ax2﹣4ax,得y=﹣3a.
∴C(1,﹣3a),∴HC=3a,又F(2,﹣4a).
∴GH=4a,GC=a.
在△BED中,∠BED=90°,若△FCD与△BED相似,则△FCD是直角三角形
∵∠FDC=∠BDE<90°,∠CFD<90°,
∴∠FCD=90°.
∴△BHC∽△CGF,
∴![]() ,
,
∴![]() ,
,
∴a2=1,
∴a=±1.
∵a>0,
∴a=1.
∴抛物线的解析式为y=x2﹣4x.


科目:初中数学 来源: 题型:
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.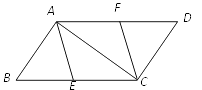
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
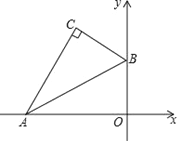
(1)若OB=6cm.①求点C的坐标;②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P; 
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由. 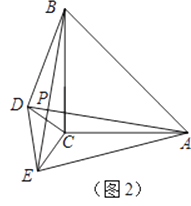
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,某校进行了宣传动员并公布了相关项目如下:
A——杆身橡筋动力模型;B——直升橡筋动力模型;C——空轿橡筋动力模型.右图为该校报名参加科技比赛的学生人数统计图.
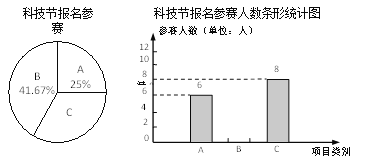
(1)该校报名参加B项目学生人数是 人;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是 °;
(3)为确定参加区科技节的学 生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,请你用学过的数学统计量分析派谁代表学校参赛?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”. 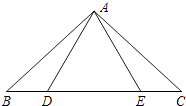
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°.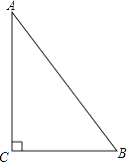
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com