
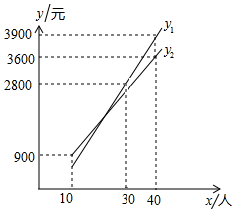
 2016年3月28日,农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路,其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选.已知河北省某旅游景点的门票为a元/人,为吸引团队游客,对团队10人以上(包含10人)的游客实行动态票价:节假日期间门票不打折,但会在团队总费用的基础上有优惠;非节假日期间门票打b折.某团队在节假日期间的门票总费用y1(元)、非节假日期间的门票总费用y2(元)与团队人数x(人)(x≥10)之间的函数关系的图象如图所示.
2016年3月28日,农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路,其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选.已知河北省某旅游景点的门票为a元/人,为吸引团队游客,对团队10人以上(包含10人)的游客实行动态票价:节假日期间门票不打折,但会在团队总费用的基础上有优惠;非节假日期间门票打b折.某团队在节假日期间的门票总费用y1(元)、非节假日期间的门票总费用y2(元)与团队人数x(人)(x≥10)之间的函数关系的图象如图所示.分析 (1)旅游待定系数法即可解决问题.
(2)由y1=710,列出方程即可解决问题.
(3)由$\left\{\begin{array}{l}{y=110x-500}\\{y=90x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=25}\\{y=2350}\end{array}\right.$,再根据图象即可解决问题.
解答 解:(1)设y1=kx+b,把(30,2800),(40,3900)代入得 $\left\{\begin{array}{l}{30k+b=2800}\\{40k+b=3900}\end{array}\right.$,
$\left\{\begin{array}{l}{30k+b=2800}\\{40k+b=3900}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=110}\\{b=-500}\end{array}\right.$,
∴y1=110x-500,
设y2=k′x+b′把(10,900),(40,3600)代入得$\left\{\begin{array}{l}{10k′+b′=900}\\{40k′+b′=3600}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k′=90}\\{b′=0}\end{array}\right.$,
∴y2=90x.
(2)当y1=710时,710=110x-500,
∴x=11.
答:他们共去了11人.
(3)由$\left\{\begin{array}{l}{y=110x-500}\\{y=90x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=25}\\{y=2350}\end{array}\right.$,
∴由图象可知:当旅游人数为25人时,节假日和非节假日的费用一样.
当10<x<25时,节假日费用便宜.
当x>25时,非节假日费用便宜.
点评 本题考查一次函数的应用、待定系数法、方程组等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会利用方程组求 两个函数的交点坐标,属于中考常考题型.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2025 | B. | 2500 | C. | 3025 | D. | 3600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2016 | B. | 2019 | C. | 6046 | D. | 6050 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com