
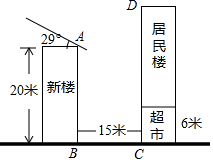
 某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)分析 (1)首先沿着光线作射线AF交CD于点F,过点F作FG⊥AB于点G.在Rt△AFG中,利用正切函数求得AG的长,进而根据CF=BG=AB-AG求得CF的高度.通过比较CF与超市高度6米,可得到中午时,超市以上的居民住房采光是否有影响.
(2)首先沿着光线作射线AE交直线BC于点E.在Rt△ABE中,利用正切函数求得BE的长,即为使得超市采光不受影响,两楼应至少相距的米数.
解答 解:(1)沿着光线作射线AF交CD于点F,过点F作FG⊥AB于点G,
由题意,在Rt△AFG中,GF=BC=15,∠AFG=29°,
∴AG=GF•tan29°=15×0.55=8.25米,
∴GB=FC=20-8.25=11.75米,
∵11.75>6,
∴居民住房会受影响;
(2)沿着光线作射线AE交直线BC于点E.
由题意,在Rt△ABE中,AB=20,∠AEB=29°,
∴BE=$\frac{AB}{tan29°}$米,
∴至少要相距37米.
点评 此题考查了三角函数的基本概念,主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
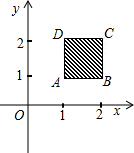 如图,在平面直角坐标系中,我们把正方形ABCD称为黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,黑色区域便由黑变白,则能够使黑色区域由黑变白的b的取值范围是3≤b≤6.
如图,在平面直角坐标系中,我们把正方形ABCD称为黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,黑色区域便由黑变白,则能够使黑色区域由黑变白的b的取值范围是3≤b≤6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
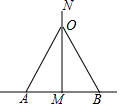 如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)
如图,一根长6.5m的电线杆,埋入地下1.5m,需要两根钢丝绳固定,已知固定点距电线杆上端N点1m,电线杆入地点距钢丝绳入地点MA=MB=3m,则两根钢丝绳的长度至少为( )(连接处忽略不计)| A. | 14m | B. | 11m | C. | 13m | D. | 10m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com