

分析 (1)连接OC,首先根据切线的性质得到∠OCP=90°,利用∠CAB=27°得到∠COB=2∠CAB=54°,然后利用直角三角形两锐角互余即可求得答案;
(2)根据OD⊥AC,从而求得∠AOE=90°-∠EAO=80°,然后利用圆周角定理求得∠ACD=$\frac{1}{2}$∠AOD=40°,最后利用三角形的外角的性质求解即可.
解答 解:(1)如图①,连接OC,
∵⊙O与PC相切于点C,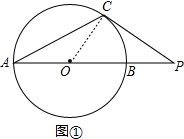
∴OC⊥PC,即∠OCP=90°,
∵∠CAB=27°,
∴∠COB=2∠CAB=54°,
在Rt△AOE中,∠P+∠COP=90°,
∴∠P=90°-∠COP=36°;
(2)∵OD⊥AC,即∠AEO=90°,
在Rt△AOE中,由∠EAO=10°,
得∠AOE=90°-∠EAO=80°,
∴∠ACD=$\frac{1}{2}$∠AOD=40°,
∵∠ACD是△ACP的一个外角,
∴∠P=∠ACD-∠A=40°-10°=30°.
点评 本题考查了切线的性质,解题的关键是能够利用圆的切线垂直于经过切点的半径得到直角三角形.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
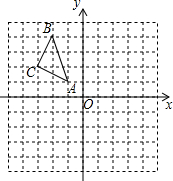 如图,A(-1,1),B(-2,4),C(-3,2).
如图,A(-1,1),B(-2,4),C(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
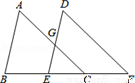
如图,点B、E、C、F在同一直线上,AC与DE相交于点G,∠A=∠D,AC∥DF,求证:AB∥DE.
查看答案和解析>>
科目:初中数学 来源:2017届湖南津市中考数学模拟试卷(2)(解析版) 题型:单选题
如图⊙O是△ABC的外接圆,∠ACO=30°,则∠B的度数是( )

A. 45° B. 50° C. 55° D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com