
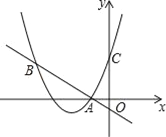
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

【答案】(1)抛物线解析式为y=x2+4x+3,一次函数解析式为y=﹣x﹣1;(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x﹣4或x≥﹣1.
【解析】(1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出太阳还是解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
解:(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0),∴0=1+m,∴m=﹣1,∴抛物线解析式为y=(x+2)2﹣1=x2+4x+3,∴点C坐标(0,3),∵对称轴x=﹣2,B、C关于对称轴对称,∴点B坐标(﹣4,3),∵y=kx+b经过点A、B,
∴![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x﹣1,
(2)由图象可知,写出满足(x+2)2+m≥kx+b的x的取值范围为x<﹣4或x>﹣1.


科目:初中数学 来源: 题型:
【题目】(本题14分)如图,抛物线y=![]() x2+
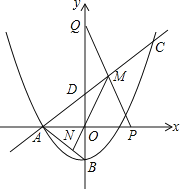
x2+![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6, ![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司手机有两类收费标准,A类收费标准如下:不管通话时间多长,少,每部手机每月必须缴月租费12元,另外,通话费按0.2元/min计。B类收费标准如下:没有月租费,但通话费按0.25元/min计。
(1)分别写出A、B两类每月应缴费用y(元)与通话时间x(min)之间的关系式;
(2)如果手机用户预算每月交55元的话费,那么该用户选择哪类收费方式合算?
(3)每月通话多长时间,按A、B两类收费标准缴费,所缴话费相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有10个红球、7个黄球、2个白球,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,然后放回去继续摸,如果前三次摸出的都是红球,那么第四次摸出( )球的可能性最大.
A.红B.黄C.白D.每种球的可能性一样大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a-2b+c<0; ③不等式ax2+bx+c>0的解集是x≥3.5; ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是![]() 中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
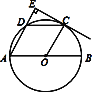
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
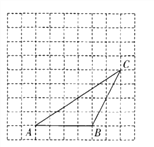
(1)请在图中画出平移后的△ABC
(2)再在图中画出△ABC的高CD
(3)![]() =
=
(4)在右图中能使![]() 的格点P的个数有 个(点P异于A) .
的格点P的个数有 个(点P异于A) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com