
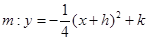 与
与 轴的交点为A、B,与
轴的交点为A、B,与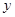 轴的交点为C,顶点为
轴的交点为C,顶点为 ,将抛物线
,将抛物线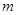 绕点B旋转
绕点B旋转 ,得到新的抛物线
,得到新的抛物线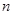 ,它的顶点为D.
,它的顶点为D.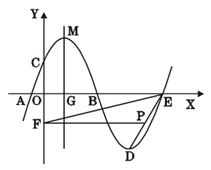
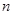 的解析式;
的解析式;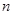 与
与 轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为
轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为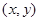 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围;
的取值范围;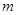 的对称轴与
的对称轴与 轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.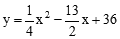 (2)S=
(2)S=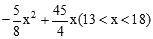 (3)直线CM与⊙G相切;证明
(3)直线CM与⊙G相切;证明 所以直线CM与⊙G相切
所以直线CM与⊙G相切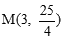 ,∴m的解析式为:
,∴m的解析式为: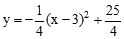
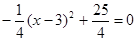 得:x1=" -2" ,x2=8 ∴
得:x1=" -2" ,x2=8 ∴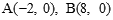
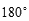 得到,∴D的坐标为
得到,∴D的坐标为
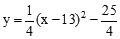 ,即
,即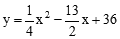
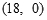 , 设直线ED的解析式为
, 设直线ED的解析式为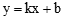 ,
,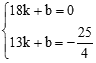 ,解得
,解得 ∴直线ED的解析式为
∴直线ED的解析式为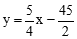
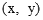 ,∴S=
,∴S=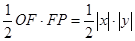 =–
=–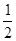 xy=
xy=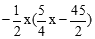
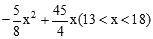
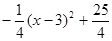 ,令
,令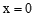 得
得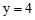 .∴
.∴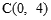
 轴的交点为G,∴OC=4,OG=3,
轴的交点为G,∴OC=4,OG=3, ∴由勾股定理得CG=5
∴由勾股定理得CG=5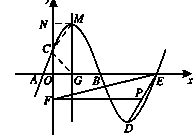

 ,
,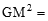
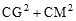 ∴根据勾股定理逆定理,得∠GCM=900
∴根据勾股定理逆定理,得∠GCM=900 ∴直线CM与⊙G相切
∴直线CM与⊙G相切 

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:不详 题型:解答题

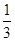 x2+bx+c经过C、D两点,求抛物线的解析式;
x2+bx+c经过C、D两点,求抛物线的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
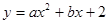 的图象与
的图象与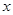 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.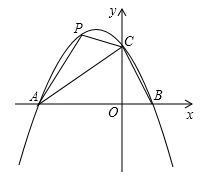
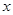 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x与BC边相交于D点.
x与BC边相交于D点.
 x经过点A,试确定此抛物线的解析式;
x经过点A,试确定此抛物线的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y2>y1 | D.y3>y1>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com