证明:(1)过点C作AC垂线交AE延长线于G,
则∠ACG=90°,
∵∠BAC=∠AFD=90°,
∴∠ABD+∠BAF=90°,∠BAF+∠CAG=90°,
∴∠ABD=∠CAG,
在△ABD和△CAG中,
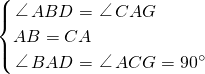
,
∴△ABD≌△CAG(ASA),
∴AD=CG,∠ADB=∠G,
当∠ADB=∠CDE时,
则∠CDE=∠G,
∵∠ACG=∠BAC=90°,
∴AB∥CG,
∴∠GCE=∠ABC=∠DCE=45°,
在△CDE和△CGE中,

,
∴△CDE≌△CGE(AAS),
∴CG=CD=AD,
∴AD=

AC,

∴当AD=

AC时,∠ADB=∠CDE;
(2)∵∠AFD=∠BAC=60°,
又∵∠AFD=∠ABD+∠BAE=60°,∠BAE+∠EAC=60°,
∴∠ABD=∠EAC,
∵AB=AC,
∴∠C=∠BAC=60°,
在△ABD和△CAE中,

,
∴△ABD≌△CAE(ASA),
∴AD=CE,∠ADB=∠AEC,
当∠ADB=∠CDE时,
则∠AEC=∠CDE,
∵∠C=∠C,
∴△CDE∽△CEA,
∴

,
∴CE
2=CD•CA,
∴AD
2=(AC-AD)•AC,
即AD
2+AD•AC-AC
2=0,
∴

(不合题意,舍去),
∴当

时,∠ADB=∠CDE.
分析:(1)首先过点C作AC垂线交AE延长线于G,由∠BAC=∠AFD=90°,易证得△ABD≌△CAG,继而可证得△CDE≌△CGE,则可得CG=CD=AD,即可得当AD=

AC时,∠ADB=∠CDE;
(2)由∠BAC=∠AFD=60°,可得△ABC是等边三角形,易证得△ABD≌△CAE(ASA),继而可得△CDE∽△CEA,然后由相似三角形的对应边成比例,求得结论.
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及等边三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.


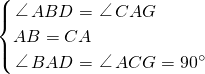 ,
, ,
, AC,
AC,
 AC时,∠ADB=∠CDE;
AC时,∠ADB=∠CDE; ,
, ,
, (不合题意,舍去),
(不合题意,舍去), 时,∠ADB=∠CDE.
时,∠ADB=∠CDE. AC时,∠ADB=∠CDE;
AC时,∠ADB=∠CDE;

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, ,连接AO、BE、DC.
,连接AO、BE、DC.