
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,OA=5,AB=2.点E在线段OC上,作∠MEN=∠AOC,使∠MEN的一边始终经过点A,另一边交线段BC于点F,连接AF.
(1)求抛物线的解析式;
(2)当点F是BC的中点时,求点E的坐标;
(3)当△AEF是等腰三角形时,求点E的坐标.
(1)y=-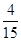 x2+
x2+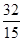 x;(2)(
x;(2)(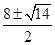 ,0);(3)(3,0)、(2,0)、(
,0);(3)(3,0)、(2,0)、(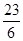 ,0).
,0).
解析试题分析:(1)根据题意可设该抛物线的解析式为:y=ax(x-8)(a≠0).然后将点A或点B的坐标代入求值即可;
(2)由相似三角形△AOE∽△ECF的对应边成比例求得线段OE的长度,则易求点E的坐标;
(3)需要分类讨论:当AE=EF、AF=EF和AE=AF时,分别求得点E的坐标.
试题解析:(1)抛物线中,AB∥OC,由对称性可知有等腰梯形AOCB.
而OA=5,AB=2,OC=8
则A(3,4),B(5,4)
抛物线的解析式是y=-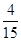 x2+
x2+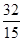 x
x
(2)可以证明△AOE∽△ECF
则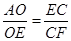 ,不妨设E(x,0),其中0≤x≤8,
,不妨设E(x,0),其中0≤x≤8,
由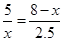 ,整理得x2-8x+12.5=0,解得
,整理得x2-8x+12.5=0,解得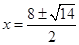
从而点E的坐标为(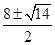 ,0)
,0)
(3)由(2)中相似还可知AO:EC=AE:EF,若△AEF为等腰三角形,则有三种可能.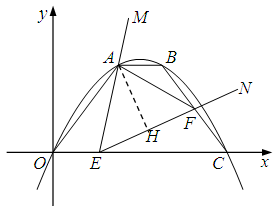
①当EA=EF时,有EC=AO=5,∴E(3,0)
②当AE=AF时,作AH⊥EF于H,有AE:EF=5:6
∴EC=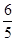 AO=6,
AO=6,
∴E(2,0)
③当FA=FE时,同理可得AE:EF=6:5
∴EC=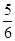 AO=
AO=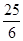 ,
,
∴E(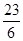 ,0)
,0)
综上所述,符合要求的点E有三个.
考点:二次函数综合题.


科目:初中数学 来源: 题型:解答题
已知二次函数 的图象经过点A(2,-3),B(-1,0).
的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)观察函数图象,要使该二次函数的图象与 轴只有一个交点,应把图象沿
轴只有一个交点,应把图象沿 轴向上平移几个单位?
轴向上平移几个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若设花园与墙平行的一边长为x(m),花园的面积为y(m2)。
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由:
(3)根据(1)中求得的函数关系式,判断当x取何值时,花园的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,二次函数y=-x2+(m-1)x+4m的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).
(1)求m的值及点A的坐标;
(2)如图,将△AEO沿x轴向右平移得到△A′E′O′,连结A′B、BE′.
①当点E′落在该二次函数的图象上时,求AA′的长;
②设AA′=n,其中0<n<2,试用含n的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
③当A′B+BE′取得最小值时,求点E′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知函数 .
.
(1)m= 时,函数图像与x轴只有一个交点;
(2)m为何值时,函数图像与x轴没有交点;
(3)若函数图像与x轴交于A、B两点,与y轴交于点C,且△ABC的面积为4,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,直线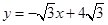 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.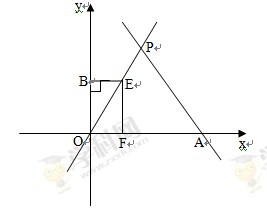
(1)求点P的坐标;
(2)请判断△OPA的形状并说明理由;
(3)请探究S与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 与
与 轴相交于
轴相交于 ,
, 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 .
.
(1)点 的坐标为 ,点
的坐标为 ,点 的坐标为 ;
的坐标为 ;
(2)在 轴的正半轴上是否存在点
轴的正半轴上是否存在点 ,使以点
,使以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出点
相似?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)b= ,c= ;
(2)选取适当的数据填写下表,并在右图的直角坐标系中画出该函数的图像;
| x | … | | | | | | … |
| y | … | | | | | | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
有两个直角三角形,在△ABC中,∠ACB=90°,AC=3,BC=6,在△DEF中,∠FDE=90°,DE=DF=4。将这两个直角三角形按图1所示位置摆放,其中直角边 在同一直线
在同一直线 上,且点
上,且点 与点
与点 重合。现固定
重合。现固定 ,将
,将 以每秒1个单位长度的速度在
以每秒1个单位长度的速度在 上向右平移,当点
上向右平移,当点 与点
与点 重合时运动停止。设平移时间为
重合时运动停止。设平移时间为 秒。
秒。
(1)当 为 秒时,
为 秒时, 边恰好经过点
边恰好经过点 ;当
;当 为 秒时,运动停止;
为 秒时,运动停止;
(2)在 平移过程中,设
平移过程中,设 与
与 重叠部分的面积为
重叠部分的面积为 ,请直接写出
,请直接写出 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)当 停止运动后,如图2,
停止运动后,如图2, 为线段
为线段 上一点,若一动点
上一点,若一动点 从点
从点 出发,先沿
出发,先沿 方向运动,到达点
方向运动,到达点 后再沿斜坡
后再沿斜坡 方向运动到达点
方向运动到达点 ,若该动点
,若该动点 在线段
在线段 上运动的速度是它在斜坡
上运动的速度是它在斜坡 上运动速度的2倍,试确定斜坡
上运动速度的2倍,试确定斜坡 的坡度,使得该动点从点
的坡度,使得该动点从点 运动到点
运动到点 所用的时间最短。(要求,简述确定点
所用的时间最短。(要求,简述确定点 位置的方法,但不要求证明。)
位置的方法,但不要求证明。)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com