
【题目】松桃孟溪火车站一检修员某天乘一辆检修车在笔直的铁轨上来回检修,规定向东为正,从车站出发到收工时,行走记录为(单位:千米):+15,-2,-5,-1,+10,-3,-2,-12,+4,+6.
⑴计算收工时,检修员在车站的哪一边,此时,距车站多远?
⑵若汽车每千米耗油0.1升,且汽油的价格为每升6.8元,求这一天检修员从出发到收工时所耗油费是多少?
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
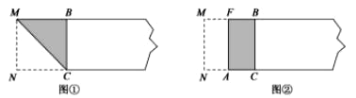
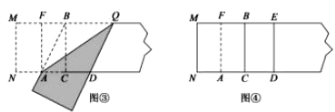
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
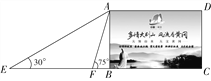
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图4所示).已知标语牌的高AB=5 m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上.求点E与点F之间的距离(计算结果精确到0.1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自![]() 月
月![]() 日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元 |
不超出 |
|
超出 |
|
超出 |
|
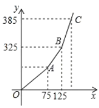
(1)若某用户![]() 月份用气量为
月份用气量为![]() ,交费多少元?
,交费多少元?
(2)调价后每月支付燃气费用![]() (单位:元)与每月用气量
(单位:元)与每月用气量![]() (单位:
(单位:![]() )的关系如图所示,求
)的关系如图所示,求![]() 与
与![]() 的解析式及
的解析式及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=108°,试解答下列问题:
(1)如图1所示,则∠O= °,并判断OB与AC平行吗?为什么?
(2)如图2,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于 °;
(3)在第(2)题的条件下,若平行移动AC,如图3.
①求∠OCB:∠OFB的值;
②当∠OEB=∠OCA时,求∠OCA的度数(直接写出答案,不必写出解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,![]() ,AC为直径,DE⊥BC,垂足为E.
,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
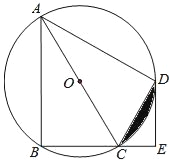
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数对“
成立的一对有理数对“![]() ,
,![]() ”为“共生有理数对”,记为
”为“共生有理数对”,记为![]() .
.
(1)通过计算判断数对“-4,2”,“7,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若![]() 是“共生有理数对”,则“
是“共生有理数对”,则“![]() ,
,![]() ”______(填“是”或“不是”)共生有理数对”,并说明理由.
”______(填“是”或“不是”)共生有理数对”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆锥的底面半径为10 cm,高为10![]() cm.
cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥侧面一周回到SA上的点M处,且SM=3AM,求它所走的最短距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com