
·ÖĪö £Ø1£©É豏¼Ē±¾µÄµ„¼ŪĪŖmŌŖ/±¾£¬øÖ±ŹµÄµ„¼ŪĪŖnŌŖ/Ö§£¬øł¾Ż”°Āņ3øö±Ź¼Ē±¾ŗĶ2Ö§øÖ±ŹŠč84ŌŖ£»Āņ4øö±Ź¼Ē±¾ŗĶ3Ö§øÖ±ŹŠč118ŌŖ”±£¬¼“æÉµĆ³ö¹ŲÓŚm”¢nµÄ¶žŌŖŅ»“Ī·½³Ģ×飬½āÖ®¼“æÉµĆ³ö½įĀŪ£»
£Ø2£©¢Ł·Ö0£¼x”Ü10ŗĶx£¾10Į½ÖÖĒéæö£¬ÓĆŗ¬xµÄŹ½×Ó±ķŹ¾y1¼“æÉ£»
¢ŚÉč»ń½±µÄѧɜӊaøö£¬¹ŗĀņ½±Ę·µÄ×ܼŪĪŖw£¬øł¾Ż×ܼŪ=µ„¼Ū”ĮŹżĮæÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾³öw£¬·ÖwøÖ±Ź£¾w±Ź¼Ē±¾”¢wøÖ±Ź=w±Ź¼Ē±¾”¢wøÖ±Ź£¼w±Ź¼Ē±¾ČżÖÖĒéæöÕŅ³ö¹ŲÓŚaµÄŅ»ŌŖŅ»“Ī²»µČŹ½£¬½āÖ®¼“æÉµĆ³ö½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©É豏¼Ē±¾µÄµ„¼ŪĪŖmŌŖ/±¾£¬øÖ±ŹµÄµ„¼ŪĪŖnŌŖ/Ö§£¬
øł¾ŻĢāŅāµĆ£ŗ$\left\{\begin{array}{l}{3m+2n=84}\\{4m+3n=118}\end{array}\right.$£¬
½āµĆ£ŗ$\left\{\begin{array}{l}{m=16}\\{n=18}\end{array}\right.$£®
“š£ŗ±Ź¼Ē±¾µÄµ„¼ŪĪŖ16ŌŖ/±¾£¬øÖ±ŹµÄµ„¼ŪĪŖ18ŌŖ/øö£®
£Ø2£©¢Łµ±0£¼x”Ü10Ź±£¬y1=18x£»
µ±x£¾10Ź±£¬y1=18”Į10+18”Į$\frac{7.5}{10}$£Øx-10£©=13.5x+45£®
×ŪÉĻĖłŹö£ŗy1=$\left\{\begin{array}{l}{18x£Ø0£¼x”Ü10£©}\\{13.5x+45£Øx£¾10£©}\end{array}\right.$£®
¢ŚÉč»ń½±µÄѧɜӊaøö£¬¹ŗĀņ½±Ę·µÄ×ܼŪĪŖw£¬
øł¾ŻĢāŅāµĆ£ŗwøÖ±Ź=13.5a+45£¬w±Ź¼Ē±¾=16a£®
µ±wøÖ±Ź£¾w±Ź¼Ē±¾Ź±£¬ÓŠ13.5a+45£¾16a£¬
½āµĆ£ŗx£¼18£»
µ±wøÖ±Ź=w±Ź¼Ē±¾Ź±£¬ÓŠ13.5a+45=16a£¬
½āµĆ£ŗx=18£»
µ±wøÖ±Ź£¾w±Ź¼Ē±¾Ź±£¬ÓŠ13.5a+45£¼16a£¬
½āµĆ£ŗx£¾18£®
“š£ŗµ±»ń½±µÄѧɜ¶ąÓŚ10øöÉŁÓŚ18øöŹ±£¬¹ŗĀņ±Ź¼Ē±¾Ź”Ē®£»µ±»ń½±µÄѧɜµČÓŚ10øöŹ±£¬¹ŗĀņ±Ź¼Ē±¾ŗĶ¹ŗĀņøÖ±ŹĖł»ØĒ®ŹżŅ»Ńł¶ą£»µ±»ń½±Ń§Éś¶ąÓŚ18øöŹ±£¬¹ŗĀņøÖ±ŹŹ”Ē®£®
µćĘĄ ±¾Ģāæ¼²éĮĖŅ»ŌŖŅ»“Ī²»µČŹ½µÄÓ¦ÓĆ”¢¶žŌŖŅ»“Ī·½³Ģ×éµÄÓ¦ÓĆŅŌ¼°Ņ»“ĪŗÆŹżµÄÓ¦ÓĆ£¬½āĢāµÄ¹Ų¼üŹĒ£ŗ£Ø1£©ÕŅ×¼µČĮæ¹ŲĻµ£¬ÕżČ·ĮŠ³ö¶žŌŖŅ»“Ī·½³Ģ×飻£Ø2£©¢Ł·Ö0£¼x”Ü10ŗĶx£¾10Į½ÖÖĒéæö£¬ÕŅ³öŗÆŹż¹ŲĻµŹ½£»¢Ś·ÖwøÖ±Ź£¾w±Ź¼Ē±¾”¢wøÖ±Ź=w±Ź¼Ē±¾”¢wøÖ±Ź£¼w±Ź¼Ē±¾ČżÖÖĒéæöĮŠ³ö¹ŲÓŚaµÄŅ»ŌŖŅ»“Ī²»µČŹ½£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2x+3=-6 | B£® | 2x-6=0 | C£® | x+3=0 | D£® | 5x-14=1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
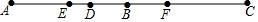 ČēĶ¼£¬µćB”¢DŌŚĻ߶ĪACÉĻ£¬BD=$\frac{1}{3}$AB=$\frac{1}{4}$CD£¬Ļ߶ĪAB”¢CDµÄÖŠµćE”¢FÖ®¼ä¾ąĄėŹĒ5cm£¬ĒóABµÄ³¤£®
ČēĶ¼£¬µćB”¢DŌŚĻ߶ĪACÉĻ£¬BD=$\frac{1}{3}$AB=$\frac{1}{4}$CD£¬Ļ߶ĪAB”¢CDµÄÖŠµćE”¢FÖ®¼ä¾ąĄėŹĒ5cm£¬ĒóABµÄ³¤£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ¦Š | B£® | 1.414 | C£® | 0 | D£® | $\frac{1}{3}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬µćPŹĒÕż·½ŠĪABCDÄŚµÄŅ»µć£¬°Ń”÷ABPČʵćBĖ³Ź±Õė·½ĻņŠż×Ŗ£¬Ź¹µćAÓėµćCÖŲŗĻ£¬µćPµÄ¶ŌÓ¦µćŹĒQ£¬ČōPA=3£¬PB=2$\sqrt{2}$£¬PC=5£¬Ēó”ĻBQCµÄ¶ČŹż£®
ČēĶ¼£¬µćPŹĒÕż·½ŠĪABCDÄŚµÄŅ»µć£¬°Ń”÷ABPČʵćBĖ³Ź±Õė·½ĻņŠż×Ŗ£¬Ź¹µćAÓėµćCÖŲŗĻ£¬µćPµÄ¶ŌÓ¦µćŹĒQ£¬ČōPA=3£¬PB=2$\sqrt{2}$£¬PC=5£¬Ēó”ĻBQCµÄ¶ČŹż£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ŗÆŹżĶ¼Ļó¾¹żµć£Ø-2£¬1£© | B£® | yĖęxµÄŌö“ó¶ų¼õŠ” | ||
| C£® | ŗÆŹżĶ¼Ļó¾¹żµŚŅ»”¢ČżĻóĻŽ | D£® | ²»ĀŪxČ”ŗĪÖµ£¬×ÜÓŠy£¼0 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com