练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：

    对于甲、乙两人的作法，可判断(　　)

    A. 甲正确，乙错误 B. 甲错误，乙正确

    C. 甲、乙均正确 D. 甲、乙均错误

    【答案】C

    【解析】试题解析：根据甲的作法作出图形，如下图所示.

    ∵四边形ABCD是平行四边形，

    ∴AD∥BC，

    ∵EF是AC的垂直平分线，

    在和中，

    ∴≌，

    又∵AE∥CF，

    ∴四边形AECF是平行四边形.

    ∴四边形AECF是菱形.

    故甲的作法正确.

    根据乙的作法作出图形，如下图所示.

    ∵AD∥BC，

    ∴∠1=∠2，∠6=∠7.

    ∵BF平分，AE平分

    ∴∠2=∠3，∠5=∠6，

    ∴∠1=∠3，∠5=∠7，

    ∵AF∥BE，且

    ∴四边形ABEF是平行四边形.

    ∵

    ∴平行四边形ABEF是菱形.

    故乙的作法正确.

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读理解：课外兴趣小组活动时，老师提出了如下问题：

    如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．

    小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．

    感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．

    （1）问题解决：受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．

    ①求证：BE+CF＞EF；②若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明；

    （2）问题拓展：如图3，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，联结EF、CF，那么下列结论①∠DCF=∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．中一定成立是 （填序号）.

    图1 图2 图3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年3月，某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动，活动结束后，随机抽取了部分同学的成绩（x均为整数，总分100分），绘制了如下尚不完整的统计图表．

    调查结果统计表

    组别

    　成绩分组（单位：分）

    　频数

    　频率

    　A

    　80≤x＜85

    　50

    　0.1

    　B

    　85≤x＜90

    　75

    　C

    　90≤x＜95

    　150

    　c

    　D

    　95≤x≤100

    　a

    　合计

    　b

    1

    根据以上信息解答下列问题：

    （1）统计表中，a=_____，b=_____，c=_____；

    （2）扇形统计图中，m的值为_____，“C”所对应的圆心角的度数是_____；

    （3）若参加本次竞赛的同学共有5000人，请你估计成绩在95分及以上的学生大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=﹣1，下列结论中： ①ab＞0，②a+b+c＞0，③当﹣2＜x＜0时，y＜0．
    正确的个数是（ ）

    A.0个
    B.1个
    C.2个
    D.3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个3×3的方格中填写了9个数字，使得每行、每列、每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．

    （1）在图1中空格处填上合适的数字，使它构成一个三阶幻方；

    （2）如图2的方格中填写了一些数和字母，当x+y的值为多少时，它能构成一个三阶幻方．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：

    组别

    成绩x分

    频数（人数）

    第1组

    25≤x＜30

    4

    第2组

    30≤x＜35

    8

    第3组

    35≤x＜40

    16

    第4组

    40≤x＜45

    a

    第5组

    45≤x＜50

    10


    请结合图表完成下列各题：
    （1）求表中a的值；
    （2）请把频数分布直方图补充完整；
    （3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
    （4）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.

    （1）求证：CE＝AD；

    （2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

    （3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，D是BA延长线上一点，E是AC的中点．
    （1）利用尺规作出∠DAC的平分线AM，连接BE并延长交AM于点F，（要求在图中标明相应字母，保留作图痕迹，不写作法）；
    （2）试判断AF与BC有怎样的位置关系与数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

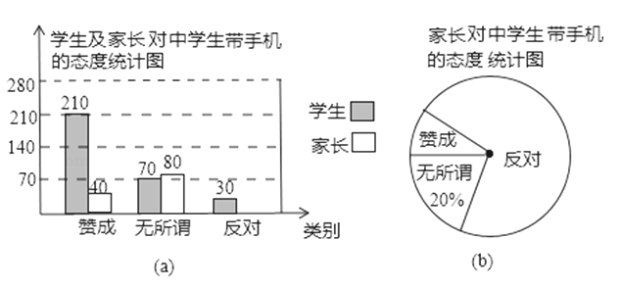
    【题目】“校园手机”现象越来越受到社会的关注，记者张丽利用周末时间随机调查了某校若干名家长对中学生带手机现象的看法，统计整理并制作了如下的统计图，根据统计图信息完成下列问题：

    （1）这次一共随机抽查了多少个学生家长进行调查；

    （2）请将条形图补充完整；在扇形统计图中表示“赞成”的圆心角等于多少度；

    （3）如果某校有3000名中学生家长，持“反对”态度的学生家长大约有多少人？

    查看答案和解析>>

    同步练习册答案