
| A. | 后者大 | B. | 前者大 | C. | 一样大 | D. | 无法确定 |
分析 根据题意,比较出2$\sqrt{7}$-2与$\sqrt{7}$的大小,即可比较出$\sqrt{7}$-1与$\frac{\sqrt{7}}{2}$的大小关系;然后根据${(2\sqrt{7}-\sqrt{7})}^{2}$=${(\sqrt{7})}^{2}$=7,22=4,7>4,可得${(2\sqrt{7}-\sqrt{7})}^{2}{>2}^{2}$,所以2$\sqrt{7}$-2>$\sqrt{7}$,因此$\sqrt{7}$-1>$\frac{\sqrt{7}}{2}$,据此解答即可.
解答 解:因为${(2\sqrt{7}-\sqrt{7})}^{2}$=${(\sqrt{7})}^{2}$=7,22=4,7>4,
所以${(2\sqrt{7}-\sqrt{7})}^{2}{>2}^{2}$,
所以2
所以2$\sqrt{7}$-2>$\sqrt{7}$,
因此$\sqrt{7}$-1>$\frac{\sqrt{7}}{2}$,
即前者大.
故选:B.
点评 此题主要考查了实数大小的比较,要熟练掌握比较的方法,解答此题的关键是通过比较2$\sqrt{7}-\sqrt{7}$的平方与2的平方的大小关系,比较出2$\sqrt{7}$-2与$\sqrt{7}$的大小关系.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:填空题
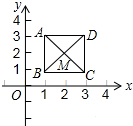 如图,已知正方形ABCD,顶点A(1,3)、B(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).
如图,已知正方形ABCD,顶点A(1,3)、B(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$与$\sqrt{(-5)^{2}}$ | B. | -3与$\frac{1}{3}$ | C. | -3与$\root{3}{-27}$ | D. | -(-2)与-|-2| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一块边长为2a m的正方形土地上,挖一个正方形的池塘,池塘四周的堤坝占地面积是4b2 m2,求当a=3.5.b=1.5时池塘的面积.
如图,在一块边长为2a m的正方形土地上,挖一个正方形的池塘,池塘四周的堤坝占地面积是4b2 m2,求当a=3.5.b=1.5时池塘的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com