
| A. | $\frac{7}{3}$米 | B. | $\frac{16}{3}$米 | C. | 14米 | D. | 6米 |
分析 根据抛物线y=-$\frac{1}{12}$x2+x+$\frac{7}{3}$可以将其等号坐标分解因式,根据实际情况x不小于0,铅球从抛出到落地一定是一个过程,刚抛出时x=0,落地时y=0,从而可以求得该同学的成绩.
解答 解:y=-$\frac{1}{12}$x2+x+$\frac{7}{3}$=$-\frac{1}{12}({x}^{2}-12x-28)=-\frac{1}{12}(x-14)(x+2)$,
当y=0时,x=-2或x=14,
∵铅球所经过的路线为抛物线y=-$\frac{1}{12}$x2+x+$\frac{7}{3}$(单位:米)的一部分,x的值应不小于0,
∴该同学的成绩是14米,
故选C.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,理论联系实际.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:解答题
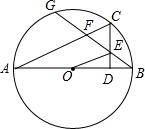 如图,AB是⊙O的直径,C是$\widehat{BG}$的中点,CD⊥AB于D,BG交CD、AC与E、F.求证:
如图,AB是⊙O的直径,C是$\widehat{BG}$的中点,CD⊥AB于D,BG交CD、AC与E、F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
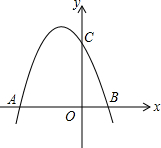 如图抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3),
如图抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com