
【题目】联想三角形内心的概念,我们可引入如下概念.
定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=![]() BP,求证:点P是△ABC的内心.
BP,求证:点P是△ABC的内心.
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=![]() AP,求∠A的度数.
AP,求∠A的度数.

【答案】应用:见解析,探究:30°
【解析】
应用:由△ABC是等边三角形,根据等边三角形的性质得到∠ABC=60°,由角平分线的性质∴∠PBE=30°,得到PE=![]() PB,因为BF是等边△ABC的角平分线,由三线合一得到BF⊥AC,PF=
PB,因为BF是等边△ABC的角平分线,由三线合一得到BF⊥AC,PF=![]() BF,证得PE=PD=PF,得到结论P是△ABC的内心;
BF,证得PE=PD=PF,得到结论P是△ABC的内心;
探究:根据题意得:PD=PC=![]() AP,由锐角三角函数得到结论.
AP,由锐角三角函数得到结论.
应用:∵△ABC是等边三角形,
∴∠ABC=60°,
∵BF为角平分线,
∴∠PBE=30°,
∴PE=![]() PB,
PB,
∵BF是等边△ABC的角平分线,
∴BF⊥AC,
∵PF=![]() BF,
BF,
∴PE=PD=PF,
∴P是△ABC的内心;
探究:根据题意得:
PD=PC=![]() AP,
AP,
∵![]() ,
,
∴∠A是锐角,
∴∠A=30°.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=![]() AB.求证:∠B=30°.
AB.求证:∠B=30°.
请填空完成下列证明.
证明:如图,作Rt△ABC的斜边上的中线CD,
则 CD=![]() AB=AD ( ).
AB=AD ( ).
∵AC=![]() AB,
AB,
∴AC=CD=AD 即△ACD是等边三角形.
∴∠A= °.
∴∠B=90°﹣∠A=30°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
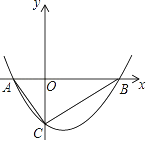
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为![]() 元/个,这种纪念品的销售价格为
元/个,这种纪念品的销售价格为![]() (元/个)与每天的销售数量
(元/个)与每天的销售数量![]() (个)之间的函数关系如图所示.
(个)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加![]() ,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
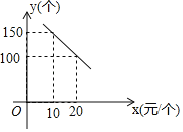
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的平面直角坐标系中,画出符合下列条件的点:
(1)画出5个纵坐标比横坐标大2的点,分别标上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)画出5个横坐标是纵坐标的2倍的点,分别标上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(3)观察上面两题所画出的点,你有什么发现,分别用语言叙述出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2,请通过计算比较S1与S2的大小.
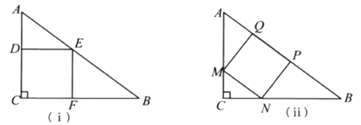
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com