
 △ABC中,∠C=90°,BC=3,AC=4,如图,现在△ABC内作一扇形,使扇形半径都在△ABC的边上,扇形的弧与△ABC的其他边相切,则符合条件的扇形的半径为________.
△ABC中,∠C=90°,BC=3,AC=4,如图,现在△ABC内作一扇形,使扇形半径都在△ABC的边上,扇形的弧与△ABC的其他边相切,则符合条件的扇形的半径为________. ,
, ,
, ,
,
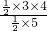 =
= .
. 为半径作扇形,扇形与AB边相切,符合题意;
为半径作扇形,扇形与AB边相切,符合题意;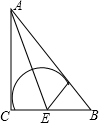


 ,
, ,
, ,故以半径
,故以半径 作扇形,符合题意;
作扇形,符合题意; =
=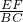 即
即 =
= .
. .
. 作扇形,符合题意;
作扇形,符合题意; ,
, .
. ,故以半径
,故以半径 作扇形,符合题意;
作扇形,符合题意; ,
, ,
, ,
, .
.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
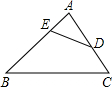 如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )
如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
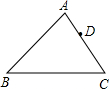 如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,
如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com