
【题目】(1)证明推断:如图(1),在正方形![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() 于点
于点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() .
.
①求证:![]() ;
;
②推断:![]() 的值为 ;
的值为 ;
(2)类比探究:如图(2),在矩形![]() 中,
中,![]() (
(![]() 为常数).将矩形
为常数).将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .试探究
.试探究![]() 与
与![]() CP之间的数量关系,并说明理由;
CP之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接![]() ,当
,当![]() 时,若
时,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
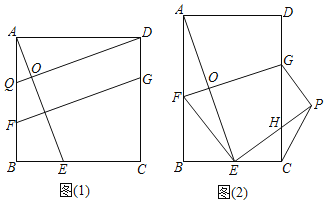
【答案】(1)①证明见解析;②解:结论:![]() .理由见解析;(2)结论:
.理由见解析;(2)结论:![]() .理由见解析;(3)
.理由见解析;(3)![]() .
.
【解析】
(1)①由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DQ.②证明四边形DQFG是平行四边形即可解决问题.
(2)结论:![]() 如图2中,作GM⊥AB于M.证明:△ABE∽△GMF即可解决问题.
如图2中,作GM⊥AB于M.证明:△ABE∽△GMF即可解决问题.
(3)如图2-1中,作PM⊥BC交BC的延长线于M.利用相似三角形的性质求出PM,CM即可解决问题.
(1)①证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ≌
≌![]()
![]() ,
,
∴![]() .
.
②解:结论:![]() .
.
理由:∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为1.
(2)解:结论:![]() .
.
理由:如图2中,作![]() 于
于![]() .
.
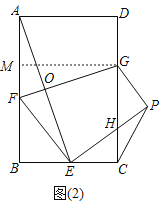
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() .
.
(3)解:如图2﹣1中,作![]() 交
交![]() 的延长线于
的延长线于![]() .
.

∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴可以假设![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或﹣1(舍弃),
或﹣1(舍弃),
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
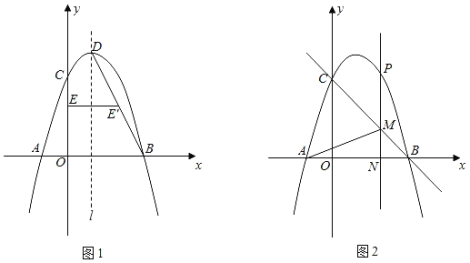
【题目】如图1,二次函数y=﹣x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l是抛物线的对称轴,D是抛物线的顶点.
(1)求该抛物线的函数表达式;
(2)如图1,连结BD,线段OC上点E关于直线l的对称点E'恰好在线段BD上,求点E的坐标;
(3)如图2,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线分别与BC交于点M,与x轴交于点N.试问:抛物线上是否存在点Q,使得△PQN与△AMN的面积相等,且线段PQ的长度最小?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
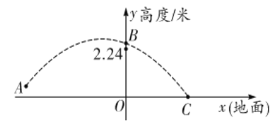
【题目】2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点![]() )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点
)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点![]() )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点
)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点![]() )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某社区工作人员在社区随机抽取了若干名居民开展环保知识有奖问答活动,并用得到的数据绘制了如图所示条形统计图(得分为整数,满分为10分,最低分为6分).
请根据图中信息,解答下列问题:
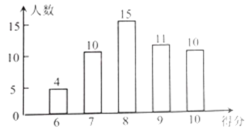
(1)本次调查一共抽取了__________名居民;
(2)求本次调查获取的样本数据的平均数;并直接写出样本数据的众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”.根据调查结果,请你帮社区工作人员直接估计出需准备多少份“一等奖”奖品.
查看答案和解析>>
科目:初中数学 来源: 题型:
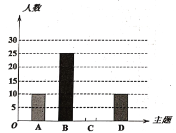
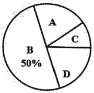
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 将一列有理数﹣1,2,﹣3,4,﹣5,6…如图所示有序排列,4所在位置为峰1,﹣9所在位置为峰2….
(1)处在峰5位置的有理数是_____;
(2)2022应排在A,B,C,D,E中_____的位置上.
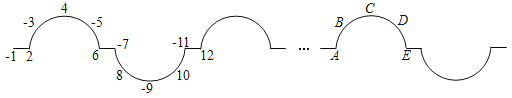
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com