
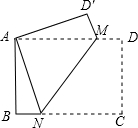
 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为$\frac{1}{3}$.
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为$\frac{1}{3}$. 分析 由$\frac{BN}{CN}$=$\frac{1}{3}$,可知$\frac{BN}{AN}$=$\frac{1}{3}$,易证AN=AM,得到$\frac{BN}{AM}$=$\frac{1}{3}$,于是可求出△AMD′的面积与△AMN的面积的比.
解答 解:根据折叠的性质,AN=CN,∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CNM=∠AMN,
∴∠ANM=∠AMN,
∴AM=AN,
∵$\frac{BN}{CN}$=$\frac{1}{3}$,得到$\frac{BN}{AM}$=$\frac{1}{3}$,
∴$\frac{BN}{AN}$=$\frac{1}{3}$,
∴$\frac{BN}{AM}$=$\frac{1}{3}$,
∴△AMD′的面积:△AMN的面积=1:3.
故答案为:$\frac{1}{3}$.
点评 本题主要考查了图形的折叠问题、等高的三角形面积比等于底的比,把△AMD′的面积与△AMN的面积的比转化为边的比,运用等高的三角形面积比等于底的比这一性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{4}$ | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,抛物线y=x2+bx+c经过点A(8,0)与点B(6,8),与x轴的另一个交点为C.
在平面直角坐标系中,抛物线y=x2+bx+c经过点A(8,0)与点B(6,8),与x轴的另一个交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 班级 节次 | 1班 | 2班 | 3班 | 4班 |
| 第1节 | 语文 | 数学 | 外语 | 化学 |
| 第2节 | 数学 | 政治 | 物理 | 语文 |
| 第3节 | 物理 | 化学 | 体育 | 数学 |
| 第4节 | 外语 | 语文 | 政治 | 体育 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
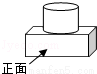
A.  B.
B.  C.
C. 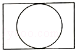 D.
D. 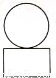
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com