顺次连接任意一个四边形、矩形、菱形、等腰梯形的四边中点,所得四边形依次是 .
【答案】
分析:三角形的中位线平行于第三边,且等于第三边的一半.需注意新四边形的形状只与对角线有关,不用考虑原四边形的形状.
解答:
解:(1)顺次连接任意一个四边形的四边中点,所得四边形是平行四边形.理由如下:
如图,已知任意四边形ABCD,E、F、G、H分别是各边中点.连接BD.
∵在△ABD中,E、H是AB、AD中点,
∴EH∥BD,EH=

BD.
∵在△BCD中,G、F是DC、BC中点,
∴GF∥BD,GF=

BD,
∴EH=GF,EH∥DF,
∴四边形EFGH为平行四边形.
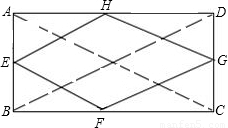
(2)顺次连接任意一个矩形的四边中点,所得四边形是菱形.理由如下:
如图,连接AC、BD.
在△ABD中,
∵AH=HD,AE=EB,
∴EH=

BD,
同理FG=

BD,HG=

AC,EF=

AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.

(3)顺次连接任意一个菱形的中点得出的四边形是矩形.理由如下:
∵E,F是中点,
∴EH∥BD,
同理,EF∥AC,GH∥AC,FG∥BD,
∴EH∥FG,EF∥GH,
则四边形EFGH是平行四边形.
又∵AC⊥BD,
∴EF⊥EH,
∴平行四边形EFGH是矩形.

(4)顺次连接任意一个等腰梯形的四边中点,所得四边形是菱形.理由如下:
连接AC、BD.
∵E、F、G、H分别是AB、BC、CD、DA的中点
∴EF=12AC,GH=12AC,EH=12BD,GF=12BD
∵AB=CD
∴AC=BD
∴EF=GH=EH=GF
∴四边形EFGH菱形.
点评:本题主要考查了三角形的中位线的性质,平行四边形的判定、矩形的判定定理、菱形的判定定理,难度适中.

 解:(1)顺次连接任意一个四边形的四边中点,所得四边形是平行四边形.理由如下:
解:(1)顺次连接任意一个四边形的四边中点,所得四边形是平行四边形.理由如下: BD.
BD. BD,
BD, (2)顺次连接任意一个矩形的四边中点,所得四边形是菱形.理由如下:
(2)顺次连接任意一个矩形的四边中点,所得四边形是菱形.理由如下: BD,
BD, BD,HG=
BD,HG= AC,EF=
AC,EF= AC,
AC, (3)顺次连接任意一个菱形的中点得出的四边形是矩形.理由如下:
(3)顺次连接任意一个菱形的中点得出的四边形是矩形.理由如下: (4)顺次连接任意一个等腰梯形的四边中点,所得四边形是菱形.理由如下:
(4)顺次连接任意一个等腰梯形的四边中点,所得四边形是菱形.理由如下:
