
【题目】某电器商店计划从厂家购进![]() 两种不同型号的电风扇,若购进8台
两种不同型号的电风扇,若购进8台![]() 型和20台
型和20台![]() 型电风扇,需资金7600元,若购进4台
型电风扇,需资金7600元,若购进4台![]() 型和15台
型和15台![]() 型电风扇,需资金5300元.
型电风扇,需资金5300元.
(1)求![]() 型电风扇每台的进价各是多少元;
型电风扇每台的进价各是多少元;
(2)该商店经理计划进这两种电风扇共50台,而可用于购买这两种电风扇的资金不超过12800元,根据市场调研,销售一台![]() 型电风扇可获利80元,销售一台
型电风扇可获利80元,销售一台![]() 型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
【答案】(1)![]() 型电风扇每台进价分别为200元、300元.;(2)当
型电风扇每台进价分别为200元、300元.;(2)当![]() 即方案一获利最大,最大利润是5120元.
即方案一获利最大,最大利润是5120元.
【解析】
(1)设![]() 型电风扇每台的进价分别为
型电风扇每台的进价分别为![]() 元、
元、![]() 元,根据条件“若购进8台
元,根据条件“若购进8台![]() 型和20台
型和20台![]() 型电风扇,需资金7600元,若购进4台
型电风扇,需资金7600元,若购进4台![]() 型和15台
型和15台![]() 型电风扇,需资金5300元 ” 可列出关于x、y的二元一次方程组,解方程组即可得出结论;
型电风扇,需资金5300元 ” 可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2) 设购进![]() 型电风扇
型电风扇![]() 台,则购进B型电风扇(50-a)台,根据总价=单价×数量结合总利润=单台利润×销售数量,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,取其内的整数即可找出各购买方案,再求出各方案获得的利润,比较后即可得出结论.
台,则购进B型电风扇(50-a)台,根据总价=单价×数量结合总利润=单台利润×销售数量,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,取其内的整数即可找出各购买方案,再求出各方案获得的利润,比较后即可得出结论.
(1)设![]() 型电风扇每台的进价分别为
型电风扇每台的进价分别为![]() 元、
元、![]() 元
元
根据题意得![]()
解得![]()
所以![]() 型电风扇每台进价分别为200元、300元.
型电风扇每台进价分别为200元、300元.
(2)设购进![]() 型电风扇
型电风扇![]() 台,
台,
由题意得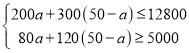
解得![]() ,
,
∴共有4种进货方案:
方案一:![]() 型
型![]()
![]() 型
型![]()
方案二: 23 27
方案三: 24 26
方案四 25 25
获利:![]()
∵![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 即方案一获利最大,最大利润是5120元.
即方案一获利最大,最大利润是5120元.


科目:初中数学 来源: 题型:
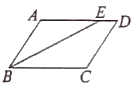
【题目】如图已知BE平分∠ABC,E点在线段AD上,∠ABE=∠AEB,AD与BC平行吗?为什么?
解:因为BE平分∠ABC(已知)
所以∠ABE=∠EBC ( )
因为∠ABE=∠AEB( )
所以∠ =∠ ( )
所以AD∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 _____________ ,(证明你的结论. )
(2)当四边形ABCD的对角线满足 __________条件时,四边形EFGH是矩形(不用证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
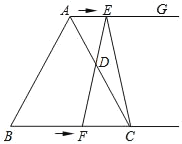
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生整体的数学学习能力,年级组织了“数学钻石活动”,从中随机抽取部分学生的成绩进行统计分析,整理得到如下不完整的频数分布表和数分布直方图:


(1)表中的![]() ,
,![]() ;
;
(2)把上面的频数分布直方图补充完整;
(3)根据调查结果,估计年级500名学生中,成绩不低于85分的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形 ABCD 绕点 A 按逆时针方向旋转到正方形AB ' C ' D ' ,旋转角为 ( 0<< 180 ) ,连接 B ' D 、 C ' D ,若 B ' D C ' D ,则 =____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这种图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?请解决以下问题:
(1)观察“规形图”,试探究∠BPC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图2:已知△ABC,BP平分∠ABC,CP平分∠ACB,直接写出∠BPC与∠A之间存在的等量关系为: .
迁移运用:如图3:在△ABC中,∠A=80°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠OPC=100°,则∠ACB的度数 .
②如图4:若D点是△ABC内任意一点,BP平分∠ABD,CP平分∠ACD.直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com