
����ABCD���ܳ�Ϊ36�����������ڽǵĶ�����Ϊ1��5��������ε����Ϊ ��
40.5 �������� ��������������������ڽǵĶ�����Ϊ1��5�������һ��30��ǣ������ܳ�Ϊ36��������εı߳�������ֱ����������30��ǵ���������ߣ��Ӷ��������� �������� ��AE��BC��E�㣬 �����������ڽǵĶ�����Ϊ1��5�� ���B=180���=30�㣬 ������ABCD���ܳ�Ϊ36�� ��AB=BC=��36=9�� ��AE=��9=�� ����... ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��4�� ����ƽ��ͼ�� ��Ԫ���Ծ� ���ͣ���ѡ��
��ͼ����C���߶�AB�ϣ���D��AC���е㣬���CD��3cm��AB��10cm����ôBC�ij�����(����)

A. 3cm B. 3.5cm C. 4cm D. 4.5cm
C ����������������������߶��е�Ķ������AC���ٸ���BC=AB��AC���㼴�ɵý⣮ �������� �ߵ�D��AC���е㣬 ��AC=2CD=2��3=6cm�� ��BC=AB��AC=10��6=4cm�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��֪������ ������A��1��0����B��-1��0����C��0��-2������������ߵĺ�������ʽ�Ͷ������꣮
������A��1��0����B��-1��0����C��0��-2������������ߵĺ�������ʽ�Ͷ������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ���ѡ��
���� �Ľ�Ϊ(�� ��)
�Ľ�Ϊ(�� ��)
A.  B.
B.  C.
C.  ��
��  D.
D.  ��
�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
��ͼ����������ABCD�У�E��AB��һ�㣬BE=2��AE=3BE��P��AC��һ���㣬��PB+PE����Сֵ��__________.
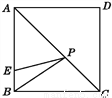
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
���������У��������ǣ� ��
A. ��������ȵ�ƽ���ı��������� B. �Խ��ߴ�ֱ���ı���������
C. �ĸ�����ȵ������������� D. �����Խ�����ȵ��ı����Ǿ���
A �����������������A.�������������Σ�B.�����������ͣ�D.�������������� ��ѡC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017���^ѧ�ڽ�ѧ����������꼶��ѧ�Ծ� ���ͣ������
һ�������Ŀڴ���װ�зֱ���к��֡������������������ϡ�����ɽ�����ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ÿ������ǰ�Ƚ������������
��1����������ȡһ�������������ϵĺ��ָպ��ǡ������ĸ��ʣ�
��2���״�����ȡһ���Żأ��ٴ�����ȡһ��������״ͼ���б��������ȡ�����������ϵĺ���ǡ����ɡ�����������ɽ���ĸ��ʣ�
��1�� P=����2�� P= ����������������1����һ�������Ŀڴ���װ�зֱ���к��֡������������������ϡ�����ɽ�����ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ֱ�����ø��ʹ�ʽ��⼴����ô𰸣� ��2�����ȸ��������оٳ����п��ܵĽ����ȡ�����������ϵĺ���ǡ����ɡ�����������ɽ��������������ø��ʹ�ʽ������ô𰸣� ��������� (1)���к��֡������������������ϡ�����ɽ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017���^ѧ�ڽ�ѧ����������꼶��ѧ�Ծ� ���ͣ���ѡ��
�������ϱ�ʾa��b����ʵ���ĵ��λ������ͼ��ʾ����a��b������a+b���Ľ��Ϊ�� ��

A��2a B��2b C��2a-2b D��-2b
B �������� ������������������֪a��0��b��0���ң����a-b��0��a+b��0���ڸ��ݾ���ֵ�����壨�����ľ���ֵ������0�ľ���ֵ��0�������ľ���ֵ�����෴������֪��=-��a-b��-=-a+b+a+b=2b�� ��ѡB�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��Ⱦ��꼶��һѧ����ĩ�����ѧ�Ծ� ���ͣ���ѡ��
��֪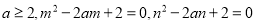 ����
����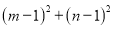 ����Сֵ�ǣ� ����
����Сֵ�ǣ� ����
A. 6 B. 3 C. -3 D. 0
A �������������������m2��2am��2��0��n2��2an��2��0�� ��m��n�ǹ���x��һԪ���η���x2��2ax��2��0���������� ��m��n��2a��mn��2�� ��(m��1)2��(n��1)2��m2��2m��1��n2��2n��1��(m��n)2��2mn��2(m��n)��2��4a2��4��4a��2��4(a��)2��3�� ��a��2�� �൱a��2ʱ��(m��1)2��(n��1)2����Сֵ...�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com