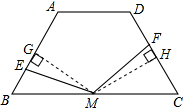
(1)证明:过点M分别作MG⊥AB,MH⊥CD,垂足为点G、H,
∵点M是边BC的中点,
∴BM=CM,
∵在梯形ABCD中,AD∥BC,AB=CD,
∴∠B=∠C=60°,
又∵MG⊥AB,MH⊥CD,
∴∠BGM=∠CHM=90°,
在△BGM与△CHM中,
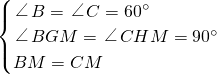
,
∴△BGM≌△CHM(AAS),
∴MG=MH,∠BMG=∠CMH=30°,
即得∠GMH=∠EMF=120°,
又∵∠EMF=∠EMG+∠GMF,且∠GMH=∠GMF+∠FMH,
∴∠EMG=∠FMH,
在△EGM与△FHM中,

,
△EGM≌△FHM(AAS),
∴ME=MF;
(2)解:当点E、F在边AB、CD上移动时,五边形AEMFD的面积的大小不会改变.
证明:∵△EGM≌△FHM,
∴S
△EMG=S
△FMH,
∴S
五边形AEMFD=S
五边形AGMHD;
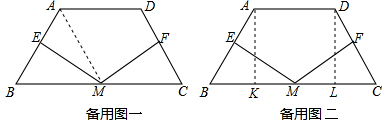
(3)解:方法一:连接AM(在备用图一),
当点E、F恰好是边AB、CD的中点,且AB=CD,得BE=CF.
又∵ME=MF,BM=CM,
∴△BEM≌△CFM(SSS),
∴∠BME=∠CMF,
∵∠EMF=120°,
∴∠BME=

(∠180°-∠EMF)=

(180°-120°)=30°,
又∵∠B=60°,
∴∠BEM=180°-60°-30°=90°,
∵点E是边AB的中点,
∴ME是边AB的垂直平分线,
∴MA=MB,
∵∠B=60°,
∴△ABM是等边三角形,
∴∠AMB=60°,
∴∠AMB=∠C.
∴AM∥CD,
又∵AD∥MC,
∴四边形AMCD是平行四边形,
∴AD=CM,
∵BC=8,BM=CM,
∴CM=4,
∴AD=CM=4.
方法二:当点E、F恰好是边AB、CD的中点,且AB=CD,得BE=CF.
又∵ME=MF,BM=CM,
∴△BEM≌△CFM(SSS),
∴∠BME=∠CMF,
∵∠EMF=120°,
∴∠BME=

(∠180°-∠EMF)=

(180°-120°)=30°,
又∵∠B=60°,
∴∠BEM=180°-60°-30°=90°,
∵∠BME=30°,
∴BE=

BM=2,
∵E是边AB的中点,
∴AB=4,
分别过点A、D作AK⊥BC,DL⊥BC,垂足为点K、L(在备用图二中).
∵∠B=60°,
∴BK=

AB=2,
同理可得,CL=2,
∴KL=8-2-2=4,
∵AK⊥BC,DL⊥BC,AD∥BC,
∴四边形AKLD是矩形,
∴AD=KL=4.
分析:(1)过点M作MG⊥AB,MH⊥CD,先利用角角边证明△BGM与△CHM全等,然后根据全等三角形对应边相等可得MG=MH,然后根据角的关系推出∠EMG=∠FMH,再利用角角边证明△EGM与△FHM全等,根据全等三角形对应边相等即可证明ME=MF;
(2)根据(1)中结论,可知S
△EMG=S
△FMH,所以点E、F移动时,五边形AEMFD的面积始终等于五边形AGMHD的面积,不变;
(3)[方法一]连接AM,然后证明△BEM与△CFM全等,根据全等三角形对应角相等得到∠BME=∠CMF,从而推出ME是AB的垂直平分线,然后证明△ABM是等边三角形,再根据等边三角形的每一个角都是60°得到∠AMB=60°,然后证明四边形AMCD是平行四边形,根据平行四边形对边相等即可求解AD=MC.
[方法二]或先证明出△BEM是直角三角形,根据直角三角形30°角所对的直角边等于斜边的一半求出BE的长度,从而得到AB的长度,再过点A作AK⊥BC,D作DL⊥BC,然后求出BK=LC=2,再根据四边形AKLD是矩形即可得解.
点评:本题综合考查了等腰梯形的性质,全等三角形的判定与性质,等边三角形的判定与性质,平行四边形的判定与性质,综合性较强,仔细分析题意作出辅助线是解题的关键,本题难度较大,对同学们能力要求较高.

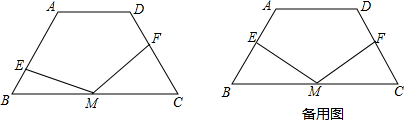
 (1)证明:过点M分别作MG⊥AB,MH⊥CD,垂足为点G、H,
(1)证明:过点M分别作MG⊥AB,MH⊥CD,垂足为点G、H,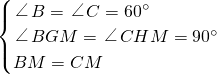 ,
, ,
, (∠180°-∠EMF)=
(∠180°-∠EMF)= (180°-120°)=30°,
(180°-120°)=30°,
 (∠180°-∠EMF)=
(∠180°-∠EMF)= (180°-120°)=30°,
(180°-120°)=30°, BM=2,
BM=2, AB=2,
AB=2,

 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.