
【题目】如图,![]() 为
为![]() 中的一条射线,点
中的一条射线,点![]() 在边
在边![]() 上,
上,![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 若
若![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据垂直于同一直线的两直线平行可得PH∥MD,再根据平行于同一直线的两直线平行可得PM∥QR,然后求出四边形PQRM是平行四边形,再求出∠MPQ=90°,根据有一个角是直角的平行四边形是矩形证明即可;
(2)根据矩形的对角线互相平分可得PS=![]() PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() .理由如下:
.理由如下:
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
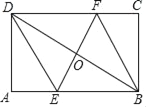
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)求证:△ADE≌△CBF;
(3)当四边形BEDF是菱形时,直接写出线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()

![]() 求该抛物线的对称轴和顶点坐标;
求该抛物线的对称轴和顶点坐标;
![]() 求抛物线与
求抛物线与![]() 轴交点的坐标;
轴交点的坐标;
![]() 画出抛物线的示意图;
画出抛物线的示意图;
![]() 根据图象回答:当
根据图象回答:当![]() 在什么范围时,
在什么范围时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围时,
在什么范围时,![]() 随
随![]() 的增大而减小?
的增大而减小?
![]() 根据图象回答:当
根据图象回答:当![]() 为何值时,
为何值时,![]() ;当
;当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲村和乙村靠近公路a、b,为了发展经济,甲乙两村准备合建一个工厂,经协商,工厂必须满足以下要求:

(1)到两村的距离相等;
(2)到两条公路的距离相等.你能帮忙确定工厂的位置吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=110°,点E、G分别是AB、AC的中点,DE⊥AB交BC于D,FG⊥AC交BC于F,连接AD、AF.试求∠DAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 为
为![]() 三条角平分线的交点,
三条角平分线的交点,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离为( )
的距离为( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com