
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.

(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
【答案】(1)点Q运动的速度是1cm/s;(2)![]() ;(3)存在,t=
;(3)存在,t=![]() 或t=
或t=![]() .
.
【解析】试题分析:(1)根据函数图象中E点所代表的实际意义求解.E点表示点P运动到与点B重合时的情形,运动时间为3s,可得AB=6cm;再由S△APQ=![]() ,可求得AQ的长度,进而得到点Q的运动速度;
,可求得AQ的长度,进而得到点Q的运动速度;
(2)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.如答图2所示,求出S的表达式,并确定t的取值范围;
(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示,求出t的值;当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示,求出t的值.
试题解析:(1)由题意,可知题图2中点E表示点P运动至点B时的情形,所用时间为3s,则菱形的边长AB=2×3=6cm.此时如答图1所示:

AQ边上的高h=ABsin60°=6×![]() =
=![]() cm, S=S△APQ=
cm, S=S△APQ=![]() AQh=
AQh=![]() AQ×3
AQ×3![]() =
=![]() ,解得AQ=3cm.∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:
,解得AQ=3cm.∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:

点Q运动至点D所需时间为:6÷1=6s,点P运动至点C所需时间为12÷2=6s,至终点D所需时间为18÷2=9s.
因此在FG段内,点Q运动至点D停止运动,点P在线段CD上继续运动,且时间t的取值范围为:6≤t≤9.过点P作PE⊥AD交AD的延长线于点E,则PE=PDsin60°=(18-2t)×![]() ,
,
S=S△APQ=![]() ADPE=
ADPE=![]() ×6×(
×6×(![]() +
+![]() )=
)=.
∴FG段的函数表达式为:S=![]() (6≤t≤9).
(6≤t≤9).
(3)菱形ABCD的面积为:6×6×sin60°=18![]() ,
,
当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示.
此时△APQ的面积S=![]() AQAPsin60°=
AQAPsin60°=![]() t2t×
t2t×![]() =
=![]() ,
,
根据题意,得![]() =
=![]() ,
,
解得:t=![]() s,
s,

当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示.
此时,有S梯形ABPQ=![]() S菱形ABCD,即
S菱形ABCD,即![]() (2t-6+t)×6×
(2t-6+t)×6×![]() =
=![]() ×18
×18![]() ,
,
解得t=![]() s,
s,
答:存在,当t=![]() 或
或![]() 时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ABC=120°,AC=4,

(1)用直尺和圆规作出△ABC的外接圆⊙O(不写作法,保留作图痕迹);
(2)求∠AOC的度数;
(3)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C.
x+2与x轴交于A、B两点,与y轴交于点C.
⑴求点A,B,C的坐标;
⑵点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
⑶此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
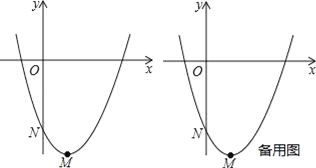
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是_____;
A.对学校的同学发放问卷进行调查
B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查
D.对在路边行走的路人随机发放问卷进行调查
并说出你的理由_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y= ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | ... | -3 | -2 | - 1 | 0 | 1 | ... |
y | ... | -6 | 0 | 4 | 6 | 6 | ... |
容易看出,(-2,0)是抛物线与x轴的一个交点,则它与x轴的另一个交点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com