
分析 先由平均数的公式计算出这组数据的平均数,再根据方差的公式计算即可.
解答 解:这组数据的平均数是(1+2+3+3+4+5)÷6=3,
方差是:$\frac{1}{6}$[(1-3)2+(2-3)2+2(3-3)2+(4-3)2+(5-3)2]=$\frac{5}{3}$;
故答案为:$\frac{5}{3}$.
点评 本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:选择题
| 成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人数 | 2 | 3 | 5 | 4 | 3 | 1 |
| A. | 9.60,9.60 | B. | 9.60,9.70 | C. | 9.70,9.60 | D. | 9.65,9.60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | (a+b)2=a2+b2 | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | D. | 5$\sqrt{5}$-$\sqrt{5}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
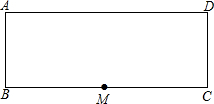 如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.
如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
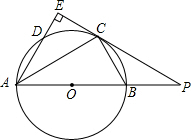 如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.
如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com