
【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
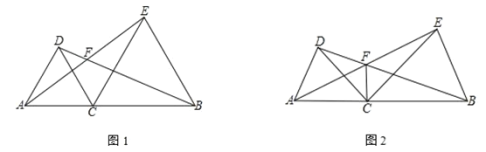
(1)如图 1,若∠ACD=60°,则∠AFD=
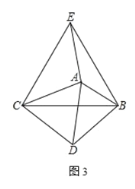
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
【答案】(1)60°.(2)90°![]() α;(3)∠EAB=140°.
α;(3)∠EAB=140°.
【解析】
(1)求出∠ACE=∠DCB,证△ACE≌△DCB,推出∠CAE=∠CDB,求出∠AFB=∠CDA+∠DAC,根据三角形内角和定理求出即可;
(2)求出∠ACE=∠DCB,证△ACE≌△DCB,推出∠CAE=∠CDB,求出∠AFB=∠CDA+∠DAC,根据三角形内角和定理求出∠AFB,然后根据圆周角定理和等腰三角形的性质即可得到结论;
(3)由△ACD是等边三角形,得到∠ACD=60°,得到∠CAB+∠CDB=360°60°80°=220°,根据全等三角形的性质得到∠CAE=∠CDB,即可得到结论.
解:(1)∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
在△ACE和△DCB中,
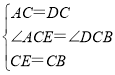 ,
,
∴△ACE≌△DCB,
∴∠CAE=∠CDB,
∴∠AFB=∠CDB+∠CDA+∠DAE
=∠CDA+∠DAE+∠BAE
=∠CDA+∠DAC
=180°60°
=120°,
∴∠AFD=60°
故答案为:60°.
(2)解:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
在△ACE和△DCB中,
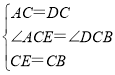 ,
,
∴△ACE≌△DCB,
∴∠CAE=∠CDB,
∴∠AFB=∠CDB+∠CDA+∠DAE
=∠CDA+∠DAE+∠BAE
=∠CDA+∠DAC
=180°∠ACD
=180°α,
∵∠CAE=∠CDB,
∴A,C,F,D四点共圆,
∴∠ADC=∠AFC,
同理∠CFB=∠BEC,
∵AC=CD,CB=CE,∠ACD=∠BCE,
∴∠ADC=∠BEC,
∴∠AFC=![]() ∠AFB=90°
∠AFB=90°![]() α;
α;
故答案为:90°![]() α;
α;
(3)∵△ACD是等边三角形,
∴∠ACD=60°,
∵∠ABD=80°,
∴∠CAB+∠CDB=360°60°80°=220°,
∵∠ACD=∠BCE,
∴∠ACE=∠BCD,
在△ACE与△BCD中,
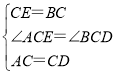 ,
,
∴△ACE≌△DCB,
∴∠CAE=∠CDB,
∴∠CAE+∠CAB=220°,
∴∠EAB=140°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°.
(1)尺规作图作出AB的垂直平分线DE,分别与AC、AB交于点D、E.并连结BD;(保留作图痕迹,不写作法)

(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如图12-1,过锐角△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:![]() ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题:
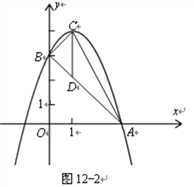
如图12-2,抛物线顶点坐标为点C(1,4),交x轴于点A,交y轴于点B(0,3).
(1)求抛物线解析式和线段AB的长度;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及![]() ;
;
(3)是否存在一点P,使S△PAB=![]() S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x | …… | 1 | 0 | 1 | 2 | 3 | 4 | …… |
ax2+bx+c | …… | 3 | 1 | 3 | …… |
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
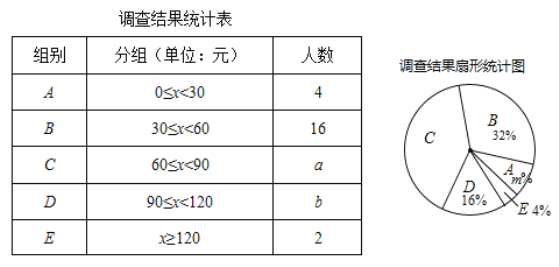
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__________人,a+b=__________,m=__________;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额在60≤x<120范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形![]() 的边长是1米;
的边长是1米;
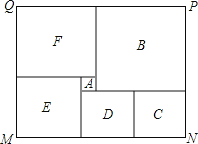
(1)若设图中最大正方形![]() 的边长是
的边长是![]() 米,请用含
米,请用含![]() 的代数式分别表示出正方形
的代数式分别表示出正方形![]() 的边长
的边长
(2)观察图形的特点可知,长方形相对的两边是相等的(即![]() ,
, ![]() )请根据以上结论,求出
)请根据以上结论,求出![]() 的值
的值
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )
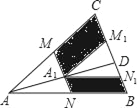
A. 14 B. 21 C. 28 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com