练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知点A（，）在函数的图象上，那么点A应在平面直角坐标系中的（     ）

    A.x轴上           B. y轴上             C. .x轴正半轴上        D.原点


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，圆内接四边形ABCD是由四个全等的等腰梯形组成，AD是⊙O的直径，则∠BEC的度数为（     　）

    A．15°     B．30°     C．45°     D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=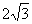，直线y=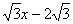经过点C，交y轴于点G。

    （1）点C、D的坐标分别是C（        ），D（        ）；

    （2）求顶点在直线y=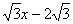上且经过点C、D的抛物线的解析式；

    （3）将（2）中的抛物线沿直线y=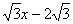平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？[源:Zxxk.Com]

    若存在，请求出此时抛物线的解析式；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    李明在一次测验中做了3道习题，请你判断他是否都正确，若有不正确，请在答题卷相应题号后写上不正确，并写出正确的解答；若正确，则只在答题卷的相应题号后写上“正确”即可。

    ①化简=

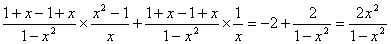
    ②解不等式组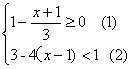   由（1）得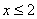   ；  由（2）得   ∴

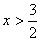    ③计算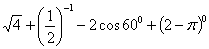=2+2-1+1=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


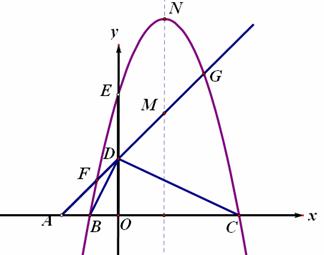
    如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点(与F、G不重合)，PQ∥y轴与抛物线交于点Q。

      (1)求经过B、E、C三点的抛物线的解析式；

      (2)判断⊿BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；

      (3)若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O的半径为2，弦AB垂直平分半径OC与D，则弦AB的长为               。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


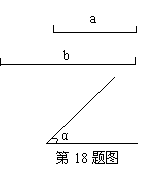
     已知：线段a,b，∠α（如图）.请用直尺和圆规作一个平行四边形，使它的两条邻边长分别等于线段a,b，它们的夹角等于∠α.要求仅用直尺和圆规作图，写出作法，并保留作图痕迹.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    使代数式有意义的的取值范围是     .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某住宅小区六月份1日至6日每天用水量变化情况如折线图所示，那么这6天的平均用水量是(    )  

    A．30吨         B． 31 吨       C．32吨         D．33吨

    查看答案和解析>>

    同步练习册答案