
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
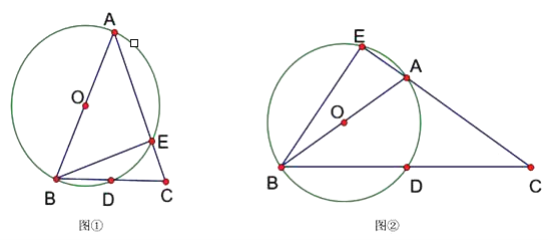
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
【答案】(1)详见解析;(2)成立,理由详见解析.
【解析】
(1)连接AD,根据直径所对的圆周角是直角,得AD⊥BC,又由AB=AC,根据等腰三角形的三线合一,得AD平分∠BAC,结合圆周角定理,即可得∠BAC=2∠CBE;
(2)连接AD.根据等腰三角形的三线合一和圆内接四边形的性质,即可证明∠BAC=2∠CBE.
(1)证明:如图①连结AD
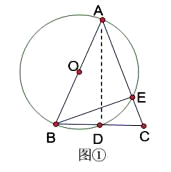
∵AB是⊙O的直径
∴AD⊥BC
∵AB=AC
∴∠CAD= ![]() ,
,
又∵BE⊥AC,
∴∠CAD=∠CBE,
∴∠CBE=![]() ;
;
(2)解:成立,理由如下:如图②连结AD,

∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴∠CAD=![]() ,
,
∵∠CAD+∠EAD=180°,∠CBE+∠EAD=180°,
∠CAD=∠CBE,
∴∠CBE=![]() .
.


科目:初中数学 来源: 题型:
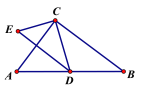
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC.
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
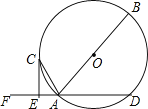
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
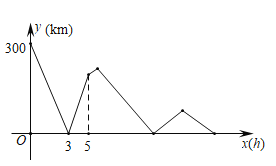
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时相向匀速行驶,当乙车到达
两地同时相向匀速行驶,当乙车到达![]() 地后,继续保持原速向远离
地后,继续保持原速向远离![]() 的方向行驶,而甲车到达
的方向行驶,而甲车到达![]() 地后,休息半小时后立即掉头,并以原速的
地后,休息半小时后立即掉头,并以原速的![]() 倍与乙车同向行驶,经过一段时间后,两车先后到达距
倍与乙车同向行驶,经过一段时间后,两车先后到达距![]() 地
地![]() 的
的![]() 地并停下来,设两车行驶的时间为
地并停下来,设两车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,
,![]() 与
与![]() 的函数关系如图,则当甲车从
的函数关系如图,则当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地__________
地__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
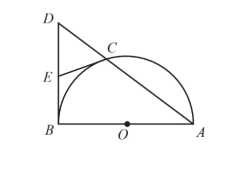
【题目】如图,AB 为半⊙O 的直径,弦 AC 的延长线与过点 B 的切线交于点 D,E 为 BD的中点,连接 CE.
(1)求证:CE 为 O 的切线;
(2)过点 C 作 CF AB ,垂足为点 F,AC=5,CF=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
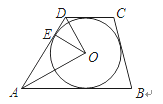
【题目】如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(1)求证:AO2=AEAD;
(2)若AO=4cm,AD=5cm,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
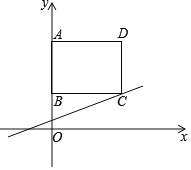
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、D的坐标分别为(0,5)、(0,2)、(4,5),直线l的解析式为y=kx+2﹣4k(k>0).
(1)当直线l经过原点O时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点C;
(3)在(1)的条件下,点M为直线l上的点,平面内是否存在x轴上方的点N,使以点O、A、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】田忌赛马是一个为人熟知的故事.传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出-匹,每匹马赛一次,赢得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强.
(1)如果齐王将马按下中上的顺序出阵比赛,那么田忌的马如何出阵才能获胜?
(2)如果齐王将马按下中上的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com