
【题目】如图,在等腰直角△ABC 中,∠ACB=90°,AC=BC,D 为 AB 中点,DE⊥DF.
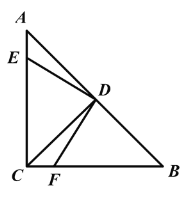
(1)图中有 对全等三角形;
(2)求证:ED=DF.
【答案】(1)3;(2)详见解析
【解析】
(1)利用等腰直角三角形的性质和三角形全等的判定解答即可;
(2)根据等腰直角三角形的性质和三角形全等的判定证明即可.
(1)∵△ABC是等腰直角三角形,且D为AB中点≌
∴CD⊥AB,且CD=BD=AD
∴∠A=∠B=∠ACD=∠BCD=45°
又∵DE⊥DF
∴∠EDF=∠ADC=∠CDB=90°,即∠ADE+∠EDC=∠CDF+∠EDC=∠CDF+∠FDB=90°
∴∠ADE =∠CDF, ∠EDC =∠FDB
由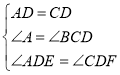 (AAS)得:AED≌CFD
(AAS)得:AED≌CFD
∴ED=FD
由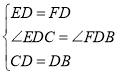 (SAS)得:CED≌BFD
(SAS)得:CED≌BFD
由![]() (ASA)得:ACD≌BCD或ACD≌CBD
(ASA)得:ACD≌BCD或ACD≌CBD
全等三角形有△AED≌CFD;CED≌BFD;ACD≌BCD或ACD≌CBD;
故答案为: 3
(2) AC BC,AD BD
CDA 90,FCD 45
AD CD
CDA ADEEDC
EDF CDFEDC
EDF CDA 90
ADE CDF
在AED与CFD中
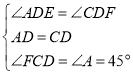
AED≌CFD
DE DF.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】![]() 地某厂和
地某厂和![]() 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,
台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,现决定给
台,现决定给![]() 地
地![]() 台,
台,![]() 地
地![]() 台,已知从
台,已知从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台,从
元每台,从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台.
元每台.
(1)设![]() 地某厂运往
地某厂运往![]() 地
地![]() 台,求总运费为多少元?
台,求总运费为多少元?
(2)在(1)中,当![]() 时,总运费是多少元?
时,总运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道![]() 表示
表示![]() 与
与![]() 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为![]() 与
与![]() 两数在数轴上所对的两点之间的距离,试探索:
两数在数轴上所对的两点之间的距离,试探索:
(1)求![]() __________.
__________.
(2)找出所有符合条件的整数![]() ,使得
,使得![]() .满足条件的所有整数值有___________
.满足条件的所有整数值有___________
(3)由以上探索,猜想对于任何有理数![]() ,
,![]() 是否有最大值或最小值?如果有最大值或最小值是多少?
是否有最大值或最小值?如果有最大值或最小值是多少?![]() 有最__________(填“最大”或“最小”)值是__________.
有最__________(填“最大”或“最小”)值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 PQ 上有一点 O,点 A 为直线外一点,连接 OA,在直线 PQ 上找一点 B,使得△AOB 是等腰三角形,这样的点 B 有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队承包了地铁某标段全长3900米的施工任务,分别从南,北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.
(1)求甲,乙两个工程队平均每天各掘进多少米?
(2)为加快工程进度两工程队都改进了施工技术,在剩余的工程中,甲工程队平均每天能比原来多掘进0.4米,乙工程队平均每天能比原来多掘进0.6米,按此施工进度能够比原来少用多少天完成任务呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程.
已知:线段 a, b.
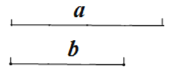
求作:等腰△ABC,使线段 a 为腰,线段 b 为底边 BC 上的高. 作法:如图,
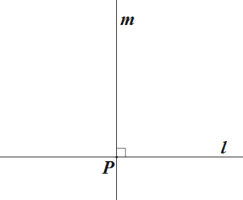
①画直线 l,作直线 m⊥l,垂足为 P;
②以点 P 为圆心,线段 b 的长为半径画弧,交直线 m 于点 A;
③以点 A 为圆心,线段 a 的长为半径画弧,交直线 l 于 B,C 两点;
④分别连接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ = ,
∴△ABC 为等腰三角形( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从货场![]() 出发,向东走2千米到达批发部
出发,向东走2千米到达批发部![]() ,继续向东走1.5千米到达商场
,继续向东走1.5千米到达商场![]() ,又向西走5.5千米到达超市
,又向西走5.5千米到达超市![]() ,最后回到货场.
,最后回到货场.
(1)以货场为原点,以东为正方向,用一个单位长度表示1千米,你能在数轴上分别表示出货场![]() ,批发部
,批发部![]() ,商场
,商场![]() ,超市
,超市![]() 的位置吗?
的位置吗?
(2)超市![]() 距离货场
距离货场![]() 多远?
多远?
(3)此货车每千米耗油0.1升,每升汽油6.20元,请计算此货车一共需要多少汽油费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划在十二年内通过公租房建设,解决低收入人群的住房问题.已知前7年,每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系构成一次函数(1≤x≤7且x为整数),且第一和第三年竣工投入使用的公租房面积分别为![]() 和
和![]() 百万平方米;后5年每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系是y=﹣
百万平方米;后5年每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系是y=﹣![]() x+
x+![]() (7<x≤12且x为整数).
(7<x≤12且x为整数).
(1)已知第6年竣工投入使用的公租房面积可解决20万人的住房问题,如果人均住房面积,最后一年要比第6年提高20%,那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题?
(2)受物价上涨等因素的影响,已知这12年中,每年竣工投入使用的公租房的租金各不相同,且第一年,一年38元/m2,第二年,一年40元/m2,第三年,一年42元/m2,第四年,一年44元/m2……以此类推,分析说明每平方米的年租金和时间能否构成函数,如果能,直接写出函数解析式;
(3)在(2)的条件下,假设每年的公租房当年全部出租完,写出这12年中每年竣工投入使用的公租房的年租金W关于时间x的函数解析式,并求出W的最大值(单位:亿元).如果在W取得最大值的这一年,老张租用了58m2的房子,计算老张这一年应交付的租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com