
【题目】计算:
(1)![]() ﹣3
﹣3 ![]() ×(
×( ![]() ﹣
﹣ ![]() )
)
(2)![]() ﹣
﹣ ![]()
![]()
(3)sin230°+2sin60°+tan45°﹣tan60°+cos230°.
【答案】
(1)解:原式=3 ![]() ﹣3
﹣3 ![]() (
( ![]() ﹣
﹣ ![]() )
)
=3 ![]() ﹣2
﹣2 ![]()
![]()
=3 ![]() ﹣
﹣ ![]()
= ![]()
(2)解:原式= ![]() +1﹣
+1﹣ ![]()
=2+1﹣2
=1
(3)解:原式=( ![]() )2+2×
)2+2× ![]() +1﹣
+1﹣ ![]() +(
+( ![]() )2
)2
= ![]() +
+ ![]() +1﹣
+1﹣ ![]() +
+ ![]()
=2
【解析】(1) 根据二次根式化简的方法将各个二次根式分别化简,然后合并括号里的同类二次根式,再计算乘法,最后计算二次根式的减法;
(2)根据二次根式的乘除法法则,先计算二次根式的乘法和除法,再将各个二次根式分别化简,最后按有理数的运算方法计算出结果;
(3)代入特殊锐角的三角函数值,然后按先乘法,再乘法最后加减的顺序计算出结果。
【考点精析】认真审题,首先需要了解二次根式的混合运算(二次根式的混合运算与实数中的运算顺序一样,先乘方,再乘除,最后加减,有括号的先算括号里的(或先去括号)),还要掌握特殊角的三角函数值(分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
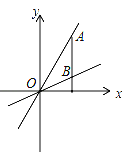
【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1 , x2是否存在实数a,使 ![]() ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
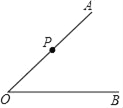
【题目】如图,点P是∠AOB的边OA上的一点:
(1)过点P画OB的垂线,垂足为H;
(2)过点H画OA的垂线,交OA于点C;
(3)再看画好垂线的图,你发现了哪个点到哪条直线的距离?分别量一量之后写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;

解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1 100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E.下列结论错误的是( )
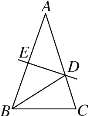
A. BD平分∠ABC B. △BCD的周长等于AB+BC
C. AD=BD=BC D. 点D是线段AC的中点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com