Question

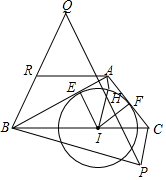
12．△ABC中，∠BAC=90°，正方形EAFI，AH⊥BC交⊙I于H，过C作HI平行线过B作其垂线交于P，等腰Rt△BPQ，AR∥BC，求证：RB=RQ．

Answer 1

分析 延长AH交BC于H，连接AH，作AN∥HI交BC于N．利用相似三角形的性质证明AN²=$\frac{1}{2}$AB•AC，再证明PB²=2AB•AC，推出PB²=4AN²，推出PB=2AN，再证明四边形ARBN是平行四边形，可得AN=BR，根据BQ=PB=2AN=2BR，即可证明．

解答 证明：延长AH交BC于H，连接AH，作AN∥HI交BC于N．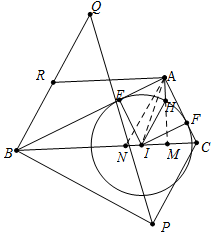

∵HI∥AN，
∴△AMN∽△HMI，
∴$\frac{AN}{HI}$=$\frac{AM}{HM}$，
∴AN=$\frac{AM•HI}{HM}$，
∵∠B=∠B，∠AMB=∠BAC，
∴△ABM∽△CBA，
∴$\frac{AM}{AC}$=$\frac{AB}{CB}$，
∴AM=$\frac{AB•AC}{BC}$，
∵四边形AEIF是正方形，
∴AI=$\sqrt{2}$EI=$\sqrt{2}$HI，
∵IM²=AI²-AM²=HI²-HM²，
∴HM²=AM²-HI²，
∵BE=AB-AE=AB-HI，
∵EI∥AC，
∴△BEI∽△BAC，
∴$\frac{EI}{AC}$=$\frac{BE}{AB}$，∵EI=IH，
∴$\frac{HI}{AC}$=$\frac{AB-HI}{AB}$，
∴HI=$\frac{AB•AC}{AB+AC}$，∵BC²=AB²+AC²，
∴AN²=$\frac{A{M}^{2}•H{I}^{2}}{H{M}^{2}}$=$\frac{\frac{A{B}^{2}•A{C}^{2}}{B{C}^{2}}•\frac{A{B}^{2}•A{C}^{2}}{（AB+AC）^{2}}}{A{M}^{2}-H{I}^{2}}$=$\frac{\frac{A{B}^{2}•A{C}^{2}}{B{C}^{2}}•\frac{A{B}^{2}•A{C}^{2}}{（AB+AC）^{2}}}{\frac{A{B}^{2}•A{C}^{2}}{B{C}^{2}}-\frac{A{B}^{2}•A{C}^{2}}{（AB+AC）^{2}}}$=$\frac{A{B}^{2}•A{C}^{2}}{（AB+AC）^{2}-B{C}^{2}}$=$\frac{A{B}^{2}•A{C}^{2}}{（AB+AC）^{2}-A{B}^{2}-A{C}^{2}}$=$\frac{AB•AC}{2}$，
∵AN∥HI∥PC，
∴∠ANM=∠BCP，
∵∠AMN=∠BPC=90°，
∴△AMN∽△BPC，
∴$\frac{BP}{AM}$=$\frac{BC}{AN}$，
∴BP²=$\frac{B{C}^{2}•A{M}^{2}}{A{N}^{2}}$=$\frac{B{C}^{2}•\frac{A{B}^{2}•A{C}^{2}}{B{C}^{2}}}{\frac{AB•AC}{2}}$=2AB•AC，
∴BP²=4AN²，
∴BP=2AN，
∵BQ∥PC∥AN，AR∥BC，
∴四边形ARBN是平行四边形，
∴BR=AN，
∵BQ=PB=2AN=2BR，
∴BR=RQ．

点评 本题考查圆综合题，相似三角形的判定和性质、平行线的性质、正方形的性质等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，本题的突破点是证明AN²=$\frac{1}{2}$AB•AC，PB²=2AB•AC，推出PB²=4AN²，题目比较难，属于竞赛题目．