
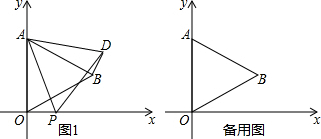
分析 (1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.
(2)由△ABD由△AOP旋转得到,△ABD≌△AOP,AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形,利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标.
(3)分三种情况进行讨论:
①当P在x轴正半轴上时,即t>0时;
②当P在x轴负半轴,但D在x轴上方时;即-$\frac{4\sqrt{3}}{3}$<t≤0时
③当P在x轴负半轴,D在x轴下方时,即t≤-$\frac{4\sqrt{3}}{3}$时.
综合上面三种情况即可求出符合条件的t的值.
解答 解:(1)如图1,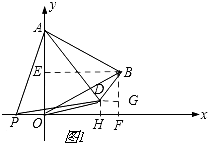
过点B作BE⊥y轴于点E,作BF⊥x轴于点F.
由已知得:BF=OE=2,
∴OF=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴点B的坐标是(2$\sqrt{3}$,2).
设直线AB的解析式是y=kx+b(k≠0),
则有$\left\{\begin{array}{l}{2\sqrt{3}k+b=2}\\{b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=4}\end{array}\right.$.
∴直线AB的解析式是y=-$\frac{\sqrt{3}}{3}$x+4,
(2)∵△ABD由△AOP旋转得到,
∴△ABD≌△AOP.
∴AP=AD,∠DAB=∠PAO.
∴∠DAP=∠BAO=60°.
∴△ADP是等边三角形.
如图2,
过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.
在Rt△BDG中,∠BGD=90°,∠DBG=60°,
∴BG=BD•cos60°=t×$\frac{1}{2}$=$\frac{t}{2}$.DG=BD•sin60°=$\frac{3}{2}$t.
∴OH=EG=2$\sqrt{3}$+$\frac{1}{2}$t,DH=2+$\frac{\sqrt{3}}{2}$t.
∴点D的坐标为(2$\sqrt{3}$+$\frac{1}{2}$t,2+$\frac{\sqrt{3}}{2}$t).
(3)存在.
假设存在点P,在它的运动过程中,使△OPD的面积等于$\frac{\sqrt{3}}{4}$.
设点P为(t,0),下面分三种情况讨论:
①当t>0时,如答图2,BD=OP=t,DG=$\frac{\sqrt{3}}{2}$t,
∴DH=2+$\frac{\sqrt{3}}{2}$t.
∵△OPD的面积等于$\frac{\sqrt{3}}{4}$,
∴$\frac{1}{2}$t(2+$\frac{\sqrt{3}}{2}$t)=$\frac{\sqrt{3}}{4}$,
∴t1=$\frac{\sqrt{21}-2\sqrt{3}}{3}$,t2=$\frac{-\sqrt{21}-2\sqrt{3}}{3}$(舍去).
∴点P1的坐标为($\frac{\sqrt{21}-2\sqrt{3}}{3}$,0).
②∵当D在x轴上时,如图3,
根据锐角三角函数求出BD=OP=$\frac{4\sqrt{3}}{3}$,
∴当-$\frac{4\sqrt{3}}{3}$<t≤0时,如答图1,BD=OP=-t,DG=-$\frac{\sqrt{3}}{2}$t,
∴GH=BF=2-(-$\frac{\sqrt{3}}{2}$t)=2+$\frac{\sqrt{3}}{2}$t.
∵△OPD的面积等于$\frac{\sqrt{3}}{4}$,
∴-$\frac{1}{2}$t(2-$\frac{\sqrt{3}}{2}$t)=$\frac{\sqrt{3}}{4}$,
∴t1=-$\frac{\sqrt{3}}{3}$,t2=-$\sqrt{3}$
∴点P2的坐标为(-$\frac{\sqrt{3}}{3}$,0),点P3的坐标为(-$\sqrt{3}$,0).
③当t≤-$\frac{4\sqrt{3}}{3}$时,BD=OP=-t,DG=-$\frac{\sqrt{3}}{2}$t,
∴DH=-$\frac{\sqrt{3}}{2}$t-2.
∵△OPD的面积等于$\frac{\sqrt{3}}{4}$,
∴$\frac{1}{2}$(-t)(-2-$\frac{\sqrt{3}}{2}$t)=$\frac{\sqrt{3}}{4}$,
∴t1=$\frac{-\sqrt{21}-2\sqrt{3}}{3}$,t2=$\frac{\sqrt{21}-2\sqrt{3}}{3}$(舍去).
∴点P4的坐标为($\frac{-\sqrt{21}-2\sqrt{3}}{3}$,0).
综上所述,点P的坐标分别为P1($\frac{\sqrt{21}-2\sqrt{3}}{3}$,0),P2(-$\frac{\sqrt{3}}{3}$,0),P3(-$\sqrt{3}$,0),P4($\frac{-\sqrt{21}-2\sqrt{3}}{3}$,0).
点评 此题是几何变换综合题,主要考查了待定系数法求函数解析式,锐角三角函数的意义,分类思想,解本题的关键是锐角三角函数的应用.


科目:初中数学 来源: 题型:解答题
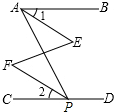 如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.
如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 5 | 6 | 4 | 2 | 1 |
| A. | 众数是2元 | B. | 中位数是2元 | C. | 极差是5元 | D. | 平均数是2.45元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
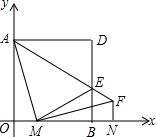 在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).
在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
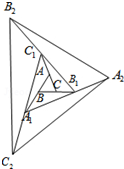 如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com