
 如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.
如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.分析 (1)把A、B两点分别代入抛物线解析可求得a和b,可求得抛物线解析式;
(2)过A作AD⊥BC于点D,则AD为⊙A的半径,由条件可证明△ABD∽△CBO,利用相似三角形的性质可求得AD的长,可求得半径,进而得出答案;
(3)由待定系数法可求得直线BC解析式,过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,可设出P、Q的坐标,可表示出△PQC和△PQB的面积,可表示出△PBC的面积,再利用二次函数的性质可求得其最大值,容易求得P点坐标.
解答 解:(1)∵抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得$\left\{\begin{array}{l}{a+b-\frac{5}{3}=0}\\{25a+5b-\frac{5}{3}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{3}$x2+2x-$\frac{5}{3}$;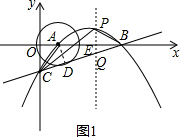
(2)相交,
理由:过A作AD⊥BC于点D,如图1,
∵⊙A与BC相切,
∴AD为⊙A的半径,
由(1)可知C(0,-$\frac{5}{3}$),且A(1,0),B(5,0),
∴OB=5,AB=OB-OA=4,OC=$\frac{5}{3}$,
在Rt△OBC中,由勾股定理可得BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{(\frac{5}{3})^{2}+{5}^{2}}$=$\frac{5\sqrt{10}}{3}$,
∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,
∴$\frac{AD}{OC}$=$\frac{AB}{BC}$,即$\frac{AD}{\frac{5}{3}}$=$\frac{4}{\frac{5\sqrt{10}}{3}}$,
解得AD=$\frac{2\sqrt{10}}{5}$,
即⊙A的半径为$\frac{2\sqrt{10}}{5}$,
∵$\frac{2\sqrt{10}}{5}$>1,
∴⊙A与y轴相交;
(3)∵C(0,-$\frac{5}{3}$),
∴可设直线BC解析式为y=kx-$\frac{5}{3}$,
把B点坐标代入可求得k=$\frac{1}{3}$,
∴直线BC的解析式为y=$\frac{1}{3}$x-$\frac{5}{3}$,
过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,如图2,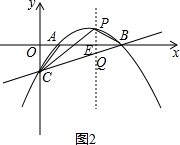
设P(x,-$\frac{1}{3}$x2+2x-$\frac{5}{3}$),则Q(x,$\frac{1}{3}$x-$\frac{5}{3}$),
∴PQ=(-$\frac{1}{3}$x2+2x-$\frac{5}{3}$)-($\frac{1}{3}$x-$\frac{5}{3}$)=-$\frac{1}{3}$x2+$\frac{5}{3}$x=-$\frac{1}{3}$(x-$\frac{5}{2}$)2+$\frac{25}{12}$,
∴S△PBC=S△PCQ+S△PBQ=$\frac{1}{2}$PQ•OE+$\frac{1}{2}$PQ•BE=$\frac{1}{2}$PQ(OE+BE)=$\frac{1}{2}$PQ•OB=$\frac{5}{2}$PQ=-$\frac{5}{6}$(x-$\frac{5}{2}$)2+$\frac{125}{24}$,
∴当x=$\frac{5}{2}$时,S△PBC有最大值$\frac{125}{24}$,此时P点坐标为($\frac{5}{2}$,$\frac{5}{4}$),
∴当P点坐标为($\frac{5}{2}$,$\frac{5}{4}$)时,△PBC的面积有最大值.
点评 本题主要考查二次函数的综合应用,涉及待定系数法、切线的性质、相似三角形的判定和性质、二次函数的性质等知识.在(1)中注意待定系数法的应用步骤,在(2)中确定出⊙A的半径是解题的关键,在(3)中用P点坐标表示出△PBC的面积是解题的关键.本题考查知识点较多,计算量大,综合性较强.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+1=(30-x)-2 | B. | x+1=(15-x)-2 | C. | x-1=(30-x)+2 | D. | x-1=(15-x)+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
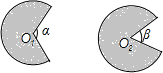 如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )
如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com