
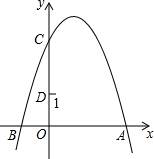
 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2). 分析 先计算出自变量为0时所对应的二次函数值得到C点坐标,则过CD中点与x轴平行的直线为y=2,再利用等腰三角形的性质得点P为直线y=2与抛物线y=-x2+2x+3的交点,然后解方程-x2+2x+3=2即可确定P点坐标.
解答 解:当x=0时,y=-x2+2x+3=3,则C(0,3),
∵△PCD是以CD为底的等腰三角形,
∴点P为直线y=2与抛物线y=-x2+2x+3的交点,
当y=2时,-x2+2x+3=2,解得x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$,
∴P点坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
故答案为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了等腰三角形的性质.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | 8岁 | B. | 9岁 | C. | 10岁 | D. | 11岁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
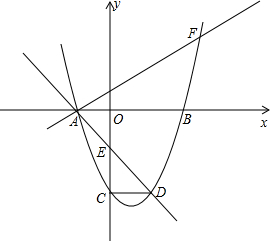 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交点为C,直线y=-x-2经过点A,交抛物线于点D,交y轴于点E,连接CD,并且∠ADC=45°.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交点为C,直线y=-x-2经过点A,交抛物线于点D,交y轴于点E,连接CD,并且∠ADC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 载货能力(箱/辆) | 运费 | |
| 甲村(元/辆) | 乙村(元/辆) | ||
| 大货车 | 70 | 800 | 900 |
| 小货车 | 35 | 400 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
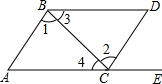 如图,点E在AC的延长线上,对于下列给出的四个条件:
如图,点E在AC的延长线上,对于下列给出的四个条件:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com