练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    直线分别与x轴，y轴交于点C、D，与反比例函数的图象交于点A、B.过点A 作AE⊥y轴与点E，过点B作BF⊥x轴与点F，连结EF，下列结论：1AD＝BC；2EF∥AB；3四边形AEFC是平行四边形；4.其中正确的个数是（ ▲ ）
    A．1             B．2              C．3               D．4

    D

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网已知：如图，直线y=-x+4分别与x轴，y轴交于A、B两点，从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（　　）
    A、2
    		10
    B、6
    C、3
    		3
    D、4+2
    		2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，直线y=kx+b分别与x轴负半轴交于点A，与y轴的正半轴交于点精英家教网B，⊙P经过点A、点B（圆心P在x轴负半轴上），已知AB=10，AP=
    254
    ．
    （1）求点P到直线AB的距离；
    （2）求直线y=kx+b的解析式；
    （3）在⊙P上是否存在点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•青浦区二模）如图，直线y=x+1分别与 x轴、y轴分别相交于点A、B．抛物线y=ax2+bx+c（a≠0）与 y轴的正半轴相交于点C，与这个一次函数的图象相交于A、D，且sin∠ACB=
    		10
    10
    ．
    （1）求点A、B、C的坐标；
    （2）如果∠CDB=∠ACB，求抛物线y=ax2+bx+c的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

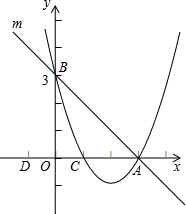    （2013•澄江县二模）如图，已知：直线m分别与x轴、y轴相交于A、B两点，抛物线y=ax2+bx+c经过A（3，0）、B（0，3）、C（1，0）三点．
    （1）求直线m的解析式；
    （2）求抛物线的解析式及对称轴；
    （3）已知D（-1，0）在x轴上．问：在直线m上是否存在一点P使△ABO与△ADP相似？若存在请求出点P的坐标，若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

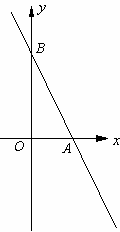
    如图，直线分别与x轴、y轴相交于A、B两点，O为坐标原点，A点的坐标为（4，0）。

    ⑴求k的值；

    ⑵若P为y轴（B点除外）上的一点，过P作PC⊥y轴交直线AB于C，设线段PC的长为l，点P的坐标为（0，m）。

    ①如果点P在线段OB（B点除外）上移动，求l与m的函数关系式，并写出自变量m的取值范围；

    ②如果点P在射线BO（B、O两点除外）上移动，连结PA，则△APC的面积S也随之发生变化。请你在面积S的整个变化过程中，求当m为何值时，S=4。

    查看答案和解析>>

    同步练习册答案