
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
【答案】![]() .
.
【解析】
试题分析:先求出∠DBE=30°,∠BDE=30°,得出BE=DE,然后设EC=x,则BE=2x,DE=2x,DC=3x,BC=![]() x,然后根据∠DAC=45°,可得AC=CD,列出方程求出x的值,然后即可求出塔DE的高度.
x,然后根据∠DAC=45°,可得AC=CD,列出方程求出x的值,然后即可求出塔DE的高度.
试题解析:由题知,∠DBC=60°,∠EBC=30°,∴∠DBE=∠DBC﹣∠EBC=60°﹣30°=30°.
又∵∠BCD=90°,∴∠BDC=90°﹣∠DBC=90°﹣60°=30°,∴∠DBE=∠BDE,∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,BC=![]() =
=![]() =
=![]() x,由题知,∠DAC=45°,∠DCA=90°,AB=20,∴△ACD为等腰直角三角形,∴AC=DC,∴
x,由题知,∠DAC=45°,∠DCA=90°,AB=20,∴△ACD为等腰直角三角形,∴AC=DC,∴![]() x+60=3x,解得:x=
x+60=3x,解得:x=![]() ,∴DE=2x=
,∴DE=2x=![]() .
.
答:塔高约为![]() m.
m.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
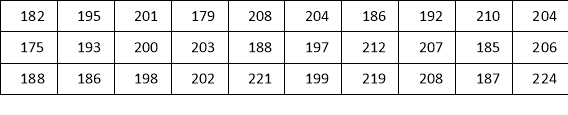
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
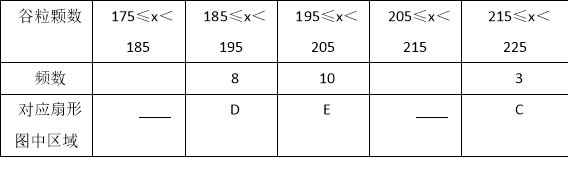
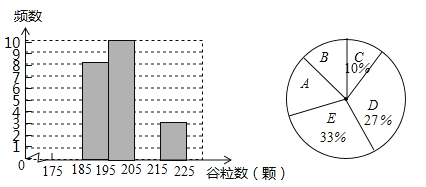
如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究: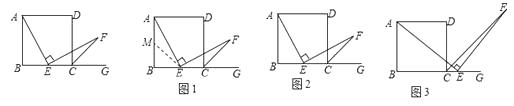
(1)、经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)、小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)、小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
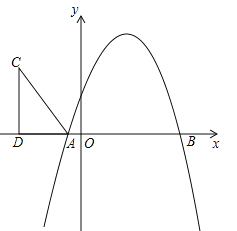
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com