
 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源:不详 题型:解答题
 ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD; ∠BAD, (1)中的结论是否仍然成立?不用证明.
∠BAD, (1)中的结论是否仍然成立?不用证明.  ∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ∥
∥ ,它们之间的距离等于
,它们之间的距离等于 .一块正方形纸板
.一块正方形纸板 的边长也等
的边长也等 .现将这块硬纸板如图所示放在两条平行线上.
.现将这块硬纸板如图所示放在两条平行线上. 上, 且
上, 且 于O, 使得直线
于O, 使得直线 与
与 、
、 相交于E、F,证明:
相交于E、F,证明: 的周长等于
的周长等于 ;
; ,使得直线
,使得直线 与
与 、
、 相交于E、F,
相交于E、F, 的周长等于
的周长等于 还成立吗?并证明你的结论;
还成立吗?并证明你的结论; 任意放置,使得直线
任意放置,使得直线 与
与 、
、 相交于E、F,直线
相交于E、F,直线 与
与 、CD相交于G,H,设
、CD相交于G,H,设 AEF的周长为
AEF的周长为 ,
, CGH的周长为
CGH的周长为 ,试问
,试问
 ,
, 和
和 之间存在着什么关系?试证明你的结论.
之间存在着什么关系?试证明你的结论.


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
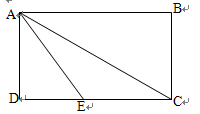
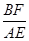 的值。
的值。查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
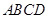 中,
中,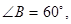 点
点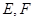 分别从点
分别从点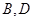 出发以同样的速度沿边
出发以同样的速度沿边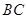 ,
,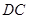 向点
向点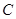 运动.给出以下四个结论:①
运动.给出以下四个结论:①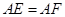 ;②
;②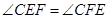 ;③当点
;③当点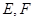 分别为边
分别为边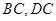 的中点时,
的中点时,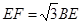 ;④当点
;④当点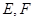 分别为边
分别为边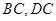 的中点时,
的中点时,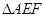 的面积最大.上述结论中正确的序号有_______.(把你认为正确的序号填在横线上)
的面积最大.上述结论中正确的序号有_______.(把你认为正确的序号填在横线上)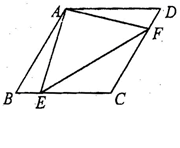
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com