
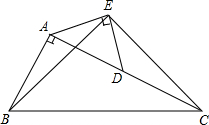
 已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.
已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想. 分析 由条件可求得AB=CD、DE=AE,且∠BAE=∠EDC=135°,可证明△ABE≌△DCE,再利用∠AEB=∠DEC,可证得BE⊥CE.
解答 解:
猜想:BE=CE,BE⊥CE.
证明如下:
∵AC=2AB,D是AC的中点,
∴CD=AB,
∵△AED为等腰直角三角形,
∴AE=DE,且∠EAD=∠EDA=45°,
∴∠BAE=∠CDE=135°,
在△ABE和△DCE中
$\left\{\begin{array}{l}{AE=DE}\\{∠BAE=∠CDE}\\{AB=CD}\end{array}\right.$
∴△ABE≌△DCE(SAS),
∴BE=CE,∠AEB=∠DEC,
∴∠BED+∠DEC=∠AEB+∠BED=∠AED=90°,
∴BE⊥CE,
即BE和CE的关系为相等且垂直.
点评 本题主要考查全等三角形的判定和性质及等腰直角三角形的判定和性质,由条件证得△ABE≌△DCE是解题的关键,注意利用等腰直角三角形的性质.


科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
一个二元码是由0和1组成的数字串x1x2…xn(n为正整数),其中xk(k=1,2,…,n)称为第k位码元,如:二元码01101的第1位码元为0,第5位码元为1。
(1)二元码100100的第4位码元为__________;
(2)二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)。已知某种二元码x1x2…x7的码元满足如下校验方程组:

其中运算 定义为:0
定义为:0 0=0,1
0=0,1 1=0,0
1=0,0 1=1,1
1=1,1 0=1。
0=1。
①计算:0 1
1 1
1 0=___________;
0=___________;
②现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了0101101,那么利用上述校验方程组可判定k等于__________。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )| A. | $\sqrt{12}$ | B. | $\sqrt{10}$ | C. | $\sqrt{8}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )
如图,在△ABC中,AB=3,AC=$\frac{9}{4}$,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么$\frac{r_1}{r_2}$=( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a3=a6 | B. | (-2a2b)3=-8a6b3 | ||
| C. | (-a2)3=a6 | D. | 12a3b2÷4a2b2=3ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com