
 ijУΪ�˽�ȫУ2000��ѧ��ÿ��ȥͼ���ʱ��������������������е�100��ѧ��������100��ѧ��ÿ��ȥͼ��ݵ�ʱ��x����λ��Сʱ��������ͳ�ƣ������������ݻ�����һ����������ͳ��ͼ����֪��ÿ��ȥͼ��ݵ�ʱ����6��x��8Сʱ��ѧ������ռ20%������������Ϣ��ͳ��ͼ����������⣺
ijУΪ�˽�ȫУ2000��ѧ��ÿ��ȥͼ���ʱ��������������������е�100��ѧ��������100��ѧ��ÿ��ȥͼ��ݵ�ʱ��x����λ��Сʱ��������ͳ�ƣ������������ݻ�����һ����������ͳ��ͼ����֪��ÿ��ȥͼ��ݵ�ʱ����6��x��8Сʱ��ѧ������ռ20%������������Ϣ��ͳ��ͼ����������⣺���� ��1��ֱ�����ó�������Ķ��塢���������Ķ���ֱ�ó��𰸣�
��2������ÿ��ȥͼ��ݵ�ʱ����6��x��8Сʱ��ѧ������ռ20%�ó���6��x��8Сʱ��ѧ�������������ó���2��x��4Сʱ��ѧ��������
��3��������������8-10Сʱ���������ó�ѧ��ÿ��ȥͼ��ݵ�ʱ��ǡ����8-10Сʱ�ĸ��ʣ�
��4��ֱ����������������������ó��𰸣�
���  �⣺��1�����ε������ڳ������飬����������100��
�⣺��1�����ε������ڳ������飬����������100��
�ʴ�Ϊ��������100��
��2��ÿ��ȥͼ��ݵ�ʱ����6��x��8Сʱ��ѧ������Ϊ��100��20%=20��
ÿ��ȥͼ��ݵ�ʱ����2��x��4Сʱ��ѧ������Ϊ��100-10-44-20-6=20��
��ͼ��ʾ��
��3��������ɵã�$\frac{6}{100}$=$\frac{3}{50}$��
�𣺳�ȡ�����ѧ��ÿ��ȥͼ��ݵ�ʱ��ǡ����8-10Сʱ�ĸ���Ϊ$\frac{3}{50}$��
��4��������ɵã�$\frac{20+6}{100}$��2000=520���ˣ���
��ȫУѧ��ÿ��ȥͼ��ݵ�ʱ�䲻����6Сʱ��������ԼΪ520�ˣ�
���� ������Ҫ�����˸��ʹ�ʽ�Լ������������������塢Ƶ���ֲ�ֱ��ͼ��֪ʶ����ȷ�ó������и��������ǽ���ؼ���


 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$\frac{1}{x}$+2 | B�� | y=-2x | C�� | y=x2+1 | D�� | y=ax+a��a�dz����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
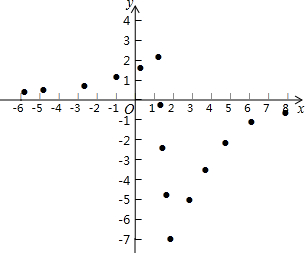 ij����ѧ��ȤС�顱����ѧϰ�����ľ��飬�Ժ���y=$\frac{-4x+6}{��x-2��^{2}}$��ͼ������ʽ�����̽����̽���������£��벹��������
ij����ѧ��ȤС�顱����ѧϰ�����ľ��飬�Ժ���y=$\frac{-4x+6}{��x-2��^{2}}$��ͼ������ʽ�����̽����̽���������£��벹���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ֱ��y=x+b��ֱ��y=kx+6���ڵ�P��1��3���������x�IJ���ʽx+b��kx+6�Ľ⼯�ǣ�������
��ͼ��ֱ��y=x+b��ֱ��y=kx+6���ڵ�P��1��3���������x�IJ���ʽx+b��kx+6�Ľ⼯�ǣ�������| A�� | x��1 | B�� | x��1 | C�� | x��3 | D�� | x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | ��2 | D�� | 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com