
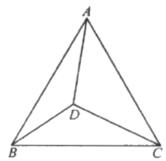
【题目】如图,点![]() 为等边三角形
为等边三角形![]() 内一点,且
内一点,且![]() ,则
,则![]() 的最小值为______.
的最小值为______.
【答案】![]()
【解析】
以CD为边在CD的右侧作等边三角形CDE,连接AE,结合等边三角形ABC可证△ACE≌△BCD,进而可证得∠AED=∠AEC-∠CED=60°,过点A作AF⊥BE于点F,利用三角函数还可求得![]() ,再根据AD与AF的大小关系可得
,再根据AD与AF的大小关系可得![]() 即
即![]() ,进而求得答案.
,进而求得答案.
解:如图,以CD为边在CD的右侧作等边三角形CDE,连接AE,

∵△CDE和△ABC为等边三角形,
∴CD=CE,AC=BC,∠DCE=∠ACB=∠CDE=∠CED=60°,
∵∠BDC=120°,
∴∠BDC+∠CDE=180°,
∴点B、D、E在同一直线上,
∵∠DCE=∠ACB,
∴∠DCE-∠ACD=∠ACB-∠ACD,
即∠ACE=∠BCD,
在△ACE与△BCD中,

∴△ACE≌△BCD(SAS),
∴AE=BD,∠AEC=∠BDC=120°,
∴∠AED=∠AEC-∠CED=60°,
过点A作AF⊥BE于点F,
在Rt△AFE中,sin∠AEF=![]() ,
,
则sin60°=![]() ,
,
当点D不与点F重合时,AD>AF,
则![]() ,
,
当点D与点F重合时,AD=AF,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值12;
②n为任意实数,x=3+n时的函数值大于x=3-n时的函数值;
③若n>3,且n是整数,当![]() 时,y的整数值有
时,y的整数值有![]() 个;
个;
④若函数图象过点![]() 和
和![]() ,其中a>0,b>0,则a<b.
,其中a>0,b>0,则a<b.
其中真命题的序号是( )
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
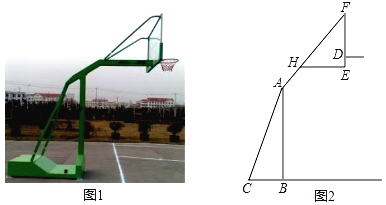
【题目】如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
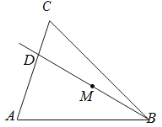
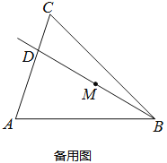
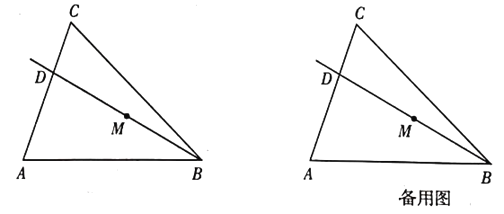
【题目】如图,在△ABC中,![]() ,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
(1)求线段BC的长;
(2)①当点D与点A、点C不重合时,过点D作DE⊥AB于点E,DF⊥BC于点F,连接ME,MF,在射线BD旋转的过程中,∠EMF的大小是否发生变化?若不变,求∠EMF的度数;若变化,请说明理由.
②在①的条件下,连接EF,直接写出△EFM面积的最小值______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,射线
,射线![]() 从与射线
从与射线![]() 重合的位置开始,绕点
重合的位置开始,绕点![]() 按顺时针方向旋转,与射线
按顺时针方向旋转,与射线![]() 重合时就停止旋转,射线
重合时就停止旋转,射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
(1)求线段![]() 的长;
的长;
(2)①当点![]() 与点
与点![]() 、点
、点![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,在射线
,在射线![]() 旋转的过程中,
旋转的过程中,![]() 的大小是否发生变化?若不变,求
的大小是否发生变化?若不变,求![]() 的度数;若变化,请说明理由.
的度数;若变化,请说明理由.
②在①的条件下,连接![]() ,直接写出
,直接写出![]() 面积的最小值____________.
面积的最小值____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
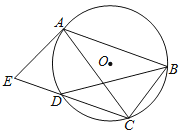
【题目】如图,四边形ABCD内接于⊙O,且AB=AC.延长CD至点E,使CE=BD,连接AE.
(1)求证:AD平分∠BDE;
(2)若AB//CD,求证:AE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
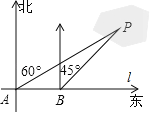
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答后面的问题.
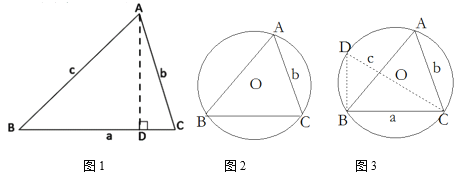
在学习了直角三角形的边角关系后,小颖和小明两个学习小组继续探究任意锐角三角形的边角关系:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
(1)小明学习小组发现如下结论:
如图1,过A作AD⊥BC于D,则sinB=![]() ,sinC=
,sinC=![]() 即AD=csinB,AD=bsinC,于是_____=______即
即AD=csinB,AD=bsinC,于是_____=______即![]() ,同理有
,同理有![]() ,
,![]()
则有![]()
(2)小颖学习小组则利用圆的有关性质也得到了类似的结论:
如图2,△ABC的外接圆半径为R,连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,
∵CD为⊙O的直径,∴∠DBC=90°,
在Rt△DBC中,
∵![]() ,
,
∴![]() ,
,![]()
同理:![]() ,
,
则有![]()
请你将这一结论用文字语言描述出来: .
小颖学习小组在证明过程中略去了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
(3)直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民,计划在三个住宅小区A、B、C之间修建一座学校,使它到三个住宅小区的距离相等,已知小区C在小区B的正东方向![]() 千米处,小区A在小区B的东北方向,且A与C之间相距
千米处,小区A在小区B的东北方向,且A与C之间相距![]() 千米,求学校到三个小区的距离及小区A在小区C的什么方向?
千米,求学校到三个小区的距离及小区A在小区C的什么方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
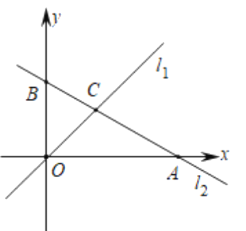

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com