
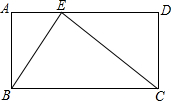
 如图,∠A=∠D=90°,AB=CD=12cm,AD=BC=25cm,点E是AD上一点,且AE=9cm,连接BE,CE.判断∠BEC的锐角、钝角还是直角,并说明理由.
如图,∠A=∠D=90°,AB=CD=12cm,AD=BC=25cm,点E是AD上一点,且AE=9cm,连接BE,CE.判断∠BEC的锐角、钝角还是直角,并说明理由. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,EQ、FQ分别是∠MEF和∠NFE的平分线,交点是Q,BP、CP分别是∠MBC和∠NCB的平分线,交点是P,F、C在AN上,B、E在AM上.如果∠Q=68°,求∠P的度数.
如图,EQ、FQ分别是∠MEF和∠NFE的平分线,交点是Q,BP、CP分别是∠MBC和∠NCB的平分线,交点是P,F、C在AN上,B、E在AM上.如果∠Q=68°,求∠P的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于F.
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,王海同学为了测量校园内一棵大树EF的高度,他走到了校园的围墙CD外(如图所示),然后他沿着过点F与墙CD垂直的直线从远处向围墙靠近至B处,使大树恰好被围墙挡住顶端C和树的顶端E时,三点在同一条直线上.若BD=2米,CD=3米,FD=8米,王海身高1.6米.求大树的高度.
如图,王海同学为了测量校园内一棵大树EF的高度,他走到了校园的围墙CD外(如图所示),然后他沿着过点F与墙CD垂直的直线从远处向围墙靠近至B处,使大树恰好被围墙挡住顶端C和树的顶端E时,三点在同一条直线上.若BD=2米,CD=3米,FD=8米,王海身高1.6米.求大树的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com