
【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
【答案】(1)△ABC和△ADC为黄金三角形,证明见解析;(2)CD=BN+CE,证明见解析.
【解析】
(1)BA=BC,且DB=DA=AC可得∠C=∠ADC=∠BAC=2∠B,∠DAC=∠B,在△ADC中由三角形内角和可求得∠B=∠DAC=36°,所以可得△ABC和△ADC为黄金三角形;
(2)由(1)可知∠BAD=∠CAD=36°,且∠AHN=∠AHE=90°,可求得∠ANH=∠AEH=54°,可得AN=AE,再借助已知利用线段的和差可得CD=BN+CE.
(1)△ABC和△ADC为黄金三角形,理由如下:
∵BA=BC,
∴∠BCA=∠BAC,
∵DA=DB,
∴∠BAD=∠B,
∵AD=AC,
∴∠ADC=∠C=∠BAC=2∠B,
∴∠DAC=∠B,
∵∠DAC+∠ADC+∠C=180°,
∴2∠B+2∠B+∠B=180°,
∴∠B=∠DAC =36°
∵△ABC和△ADC为等腰三角形,顶角∠B=∠DAC =36°
∴△ABC和△ADC为黄金三角形;
(2)CD=BN+CE.证明如下:
在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°,
在△ACD中,∵AD=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,
∴∠BAD=∠CAD=36°,
∵MH⊥AD,
∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,
∴AN=AE,
又∵BA=BC,DB=AC,
∴BN=AB-AN=BC-AE,CE=AE-AC=AE-BD,
∴BN+CE=BC-BD=CD,
即CD=BN+CE.


科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
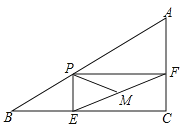
【题目】在Rt△ABC中,∠C=90°,AB=5,AC=3,点P为边AB上一动点(且点P不与点A,B重合),PE⊥BC于E,PF⊥AC于F,点M为EF中点,则PM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() -(k+2)x+2k=0.
-(k+2)x+2k=0.
(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰![]() 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
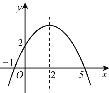
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2-4ac<0;②ab>0;③a-b+c=0;④4a+b=0;⑤当y=2时,x只能等于0.其中正确的是( )
A. ①④ B. ③④ C. ②⑤ D. ③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
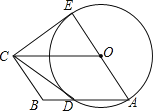
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com