Question

已知正整数a、b之差为120，它们的最小公倍数是其最大公约数的105倍，那么，a、b中较大的数是    ．

Answer 1

【答案】分析：根据已知条件，可设（a，b）=d，则a=md，b=nd，于是a、b的最小公倍数为mnd，将条件代入数值，组成方程组，然后用列举法写出所有符合条件的数，再找出正确答案即可解答．
解答：解：设（a，b）=d，且a=md，b=nd，其中m＞n，且m与n互质，
于是a、b的最小公倍数为mnd，
依题意有
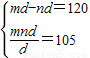
即，
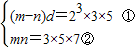
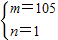
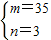
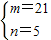
则m＞n据②可得或或或
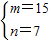
根据①只取
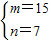
可求得d=15，故两个数中较大的数是md=225．
点评：本题主要考查最大公约数与最小公倍数的关系，列举法能够写出所有符合条件的数，再一一排除即可．