
 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转90°,得到△CBP′,
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转90°,得到△CBP′,分析 (1)根据正方形的性质得BA=BC,∠ABC=90°,则△ABP绕点B顺时针旋转90°得到△CBP′,作P′B⊥PB,且P′B=PB即可得到△CBP′;
(2)先根据三角形内角和计算出∠BPA的度数,然后根据旋转的性质求∠PBP′和∠BP′C的度数.
解答 解:(1)如图,△CBP′为所作;
(2)在△ABP中,∠APB=180°-∠ABP-∠BAP=180°-35°-20°=125°,
∵△ABP绕点B顺时针旋转90°,得到△CBP′,
∴BP=BP′,∠PBP′=90°,∠BP′C=∠BPA=125°.
点评 本题考查了作图=旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了正方形的性质.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
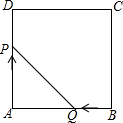 如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )
如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.某大街水平地画有两路灯灯秆AB=CD=10米,小明晚上站在两灯杆的正中位置观察眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知底面到小明眼睛处的高度EF=1.5米;
如图.某大街水平地画有两路灯灯秆AB=CD=10米,小明晚上站在两灯杆的正中位置观察眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知底面到小明眼睛处的高度EF=1.5米;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com