
如图中,△ABC外接圆的圆心的坐标是________.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 AB.
AB.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
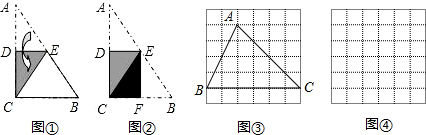
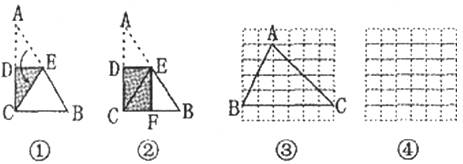
(1)图①是一块直角三角形纸片.将该三角形纸片按如图①方法折叠,其中点A与点C重合,DE为折痕.试证明△CBE是等腰三角形;
(2)再将图①中的△CBE沿对称轴EF折叠(如图②).通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”.你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;
(3)请在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;
(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上).请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件时,一定能折成组合矩形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com