
【题目】如图,在平面直角坐标系中,顶点为(![]() ,
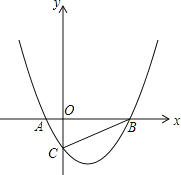
,![]() )的抛物线交y轴于点C(0,﹣2),交x轴于点A,B(点A在点B的左侧).P点是y轴上一动点,Q点是抛物线上一动点.
)的抛物线交y轴于点C(0,﹣2),交x轴于点A,B(点A在点B的左侧).P点是y轴上一动点,Q点是抛物线上一动点.
(1)求抛物线的解析式;
(2)P点运动到何位置时,△POA与△ABC相似?并求出此时P点的坐标;
(3)当以A、B、P、Q四点为顶点的四边形为平行四边形时,求Q点的坐标.
【答案】(1)抛物线为![]() ;(2)P点的坐标为(0,±2),(0,±
;(2)P点的坐标为(0,±2),(0,±![]() );(3)(﹣5,18),(5,3),(3,﹣2).
);(3)(﹣5,18),(5,3),(3,﹣2).
【解析】
(1)设顶点式抛物线解析式,将点C的坐标代入即可;
(2)先求出点A、B的坐标,证明△ACB是直角三角形,分两种对应关系利用三角形相似求出点P的坐标;
(3)分三种情况:①Q点的横坐标为﹣5;②Q点的横坐标为5;③Q点的横坐标为﹣1+4=3;代入抛物线的解析式求出它们的纵坐标,从而求得Q点的坐标.
解:(1)设抛物线为y=a(x﹣![]() )2﹣
)2﹣![]() ,
,
∵抛物线经过点C(0,﹣2),
∴﹣2=a(0﹣![]() )2﹣
)2﹣![]() ,
,
a=![]() .
.
∴抛物线为![]() ;
;
(2)在原解析式中,令y=0,则![]() x2﹣
x2﹣![]() x﹣2=0,
x﹣2=0,
解得x1=﹣1,x2=4,
则点A为(﹣1,0),点B为(4,0),
则AB=5,AC=![]() ,BC=2
,BC=2![]() ,
,
∵(![]() )2+(2
)2+(2![]() )2=52,
)2=52,
∴△ACB是直角三角形,
①设OP的长为x,则有
![]() ,
,
解得x=2;
②设OP的长为y,则有
![]() ,
,
解得y=![]() ;
;
则P点的坐标为(0,±2),(0,±![]() );
);
(3)因为以A、B、P、Q四点为顶点的四边形为平行四边形,
所以分三种情况:
①Q点的横坐标为﹣5,y=![]() ×(﹣5)2﹣
×(﹣5)2﹣![]() ×(﹣5)﹣2=18;
×(﹣5)﹣2=18;
②Q点的横坐标为5,y=![]() ×52﹣
×52﹣![]() ×5﹣2=3;
×5﹣2=3;
③Q点的横坐标为﹣1+4=3,y=![]() ×32﹣
×32﹣![]() ×3﹣2=﹣2.
×3﹣2=﹣2.
所以Q点的坐标为(﹣5,18),(5,3),(3,﹣2).


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,BE平分
中,BE平分![]() 交AD于点E.
交AD于点E.

(1)如图1,若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,过点A作![]() ,交DC的延长线于点F,分别交BE,BC于点G,H,且
,交DC的延长线于点F,分别交BE,BC于点G,H,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
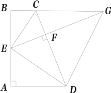
【题目】如图,已知四边形ABCD中,AB⊥AD,BC∥AD,E为AB的中点,且EC、ED分别为∠BCD、∠ADC的角平分线,EF⊥CD交BC的延长线于点G,连接DG.
(1)求证:CE⊥DE;
(2)若AB=6,求CF·DF的值;
(3)当△BCE与△DFG相似时,![]() 的值是 .
的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
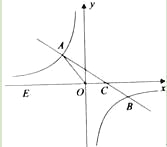
【题目】如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字1、2、3、4,将卡片背面朝上,洗匀后从中任意抽取1张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号为1、2、3的3个小球,这些球除标号外都相同,搅匀后从中任意摸出1个球,将摸到的球的标号作为减数.
(1)求这两个数的差为0的概率;
(2)游戏规则规定:当抽到的这两个数的差为非负数时,甲获胜;否则,乙获胜.这样的规则公平吗?如果不公平,请设计一个公平的规则,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人,原计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: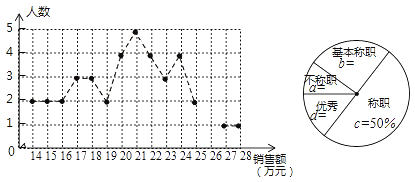
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的可视点.
(1)当⊙O的半径为1时,
①在点![]() 、E(1,1)、F(3,0)中,⊙O的可视点是______.
、E(1,1)、F(3,0)中,⊙O的可视点是______.
②过点M(4,0)作直线l:y=kx+b,若直线l上存在⊙O的可视点,求b的取值范围;
(2)若T(t,0),⊙T的半径为1,直线y=![]() 上存在⊙T的可视点,且所有可视点构成的线段长度为n,若
上存在⊙T的可视点,且所有可视点构成的线段长度为n,若![]() ,直接写出t 的取值范围.
,直接写出t 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com