
【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题. 
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地由于居民增多,要在公路边增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠ACB=2∠B,∠C=90°,AD为∠BAC的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)



(2)如图2,当∠C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.
(3)如图3,当∠ACB≠90°,∠ACB=2∠B ,AD为△ABC的外角∠CAF的平分线,交BC的延长线于点D,则线段 AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点O按顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工程队从A点出发,沿北偏西67°方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23°的方向继续修建BC段,到达C点又改变方向,从C点继续修建CE段,若使所修路段CE∥AB,∠ECB应为多少度?试说明理由.此时CE与BC有怎样的位置关系?
以下是小刚不完整的解答,请帮她补充完整.
解:由已知,根据
得∠1=∠A=67°
所以,∠CBD=23°+67°= °;
根据
当∠ECB+∠CBD= °时,可得CE∥AB.
所以∠ECB= °
此时CE与BC的位置关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6). 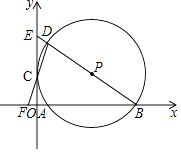
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com