
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E. 
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
【答案】
(1)证明:连接OD,
∵BC是⊙O的切线,
∴∠ABC=90°,
∵CD=CB,
∴∠CBD=∠CDB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODC=∠ABC=90°,
即OD⊥CD,
∵点D在⊙O上,
∴CD为⊙O的切线

(2)解:在Rt△OBF中,
∵∠ABD=30°,OF=1,
∴∠BOF=60°,OB=2,BF= ![]() ,
,
∵OF⊥BD,
∴BD=2BF=2 ![]() ,∠BOD=2∠BOF=120°,
,∠BOD=2∠BOF=120°,
∴S阴影=S扇形OBD﹣S△BOD= ![]() ﹣
﹣ ![]() ×2
×2 ![]() ×1=
×1= ![]() π﹣
π﹣ ![]() .
.

【解析】(1)首先连接OD,由BC是⊙O的切线,可得∠ABC=90°,又由CD=CB,OB=OD,易证得∠ODC=∠ABC=90°,即可证得CD为⊙O的切线;(2)在Rt△OBF中,∠ABD=30°,OF=1,可求得BD的长,∠BOD的度数,又由S阴影=S扇形OBD﹣S△BOD , 即可求得答案.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
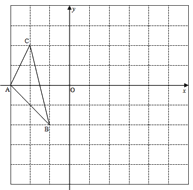
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=﹣1
当x+3<0时,原方程可化为:x+3=﹣2,解得x=﹣5
所以原方程的解是x=﹣1,x=﹣5
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当b为何值时,方程|x﹣2|=b ①无解;②只有一个解;③有两个解.
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
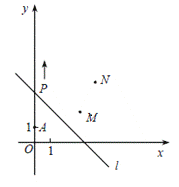
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿![]() 轴以每秒1个单位长的速度向上移动,且过点P的直线
轴以每秒1个单位长的速度向上移动,且过点P的直线![]() 也随之移动,设移动时间为
也随之移动,设移动时间为![]() 秒.
秒.
(1)当![]() 时,求直线的解析式;
时,求直线的解析式;
(2)若点M,N位于直线的异侧,确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
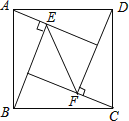
【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A. 7 B. 8 C. 7![]() D. 7
D. 7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C在数轴上对应的实数分别为a、b、c,满足(b+5)2+|a﹣8|=0,点P位于该数轴上.
(1)求出a,b的值,并求A、B两点间的距离;
(2)设点C与点A的距离为25个单位长度,且|ac|=﹣ac.若PB=2PC,求点P在数轴上对应的实数;
(3)若点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…(以此类推).则点p 能移动到与点A或点B重合的位置吗?若能,请探究需要移动多少次重合?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:
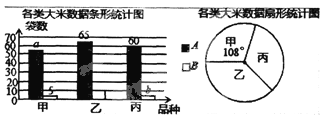
根据所给信息,解决下列问题:
(1)a=_______,b=_______.
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?请简述理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x= ![]() .
.
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F. 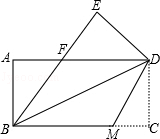
(1)求证:△ABF≌△EDF;
(2)若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com