
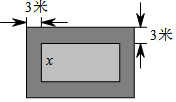
 һ��־�Խ����ĵ���ʳ����Σ����ǿ���2���������������ϻ����ң��γ�һ���߿�Ϊ3�ij����ο���ͼ��ʾ������֪�������ǡ������504��߳�Ϊ0.5���������ң��ӷ���Բ��ƣ�������˱�־�Խ������泤���εĿ�Ϊx�ף��������з��̣�
һ��־�Խ����ĵ���ʳ����Σ����ǿ���2���������������ϻ����ң��γ�һ���߿�Ϊ3�ij����ο���ͼ��ʾ������֪�������ǡ������504��߳�Ϊ0.5���������ң��ӷ���Բ��ƣ�������˱�־�Խ������泤���εĿ�Ϊx�ף��������з��̣�| A�� | �� | B�� | �� | C�� | �ڢ� | D�� | �٢ڢ� |
 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��a��b��c��d����֪c��a��c��b��ֱ��b��c��d����һ�㣬����1=50�㣬���2=50�㣮
��ͼ��ֱ��a��b��c��d����֪c��a��c��b��ֱ��b��c��d����һ�㣬����1=50�㣬���2=50�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
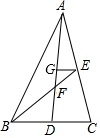 ��ͼ���ڡ�ABC�У�����AD��BE�ཻ�ڵ�F��EG��BC����AD�ڵ�G����S��EFG��S��ABC�ı�Ϊ��������
��ͼ���ڡ�ABC�У�����AD��BE�ཻ�ڵ�F��EG��BC����AD�ڵ�G����S��EFG��S��ABC�ı�Ϊ��������| A�� | $\frac{1}{12}$ | B�� | $\frac{1}{18}$ | C�� | $\frac{1}{24}$ | D�� | $\frac{1}{36}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
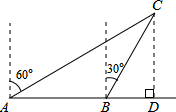 ��ͼ��һ�洬�����������У���A���ú���Cλ�ڱ�ƫ��60��ķ���ǰ��20���ﵽ��B�㣬��ʱ����ú���Cλ�ڱ�ƫ��30��ķ�����C������AB�ľ���CD��
��ͼ��һ�洬�����������У���A���ú���Cλ�ڱ�ƫ��60��ķ���ǰ��20���ﵽ��B�㣬��ʱ����ú���Cλ�ڱ�ƫ��30��ķ�����C������AB�ľ���CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���Ϊ3�������εij� | B�� | ��Ϊ3����Ϊ2�ij����εĶԽ��߳� | ||
| C�� | ���Ϊ8����������ⳤ | D�� | �Խ��߷ֱ�Ϊ2��4�����α߳� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com