
【题目】某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.
(1)分别求出y1、y2与x的函数关系式,并确定x的取值范范围;
(2)分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)
(3)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
【答案】(1)y1=(m+6)x﹣8(0≤x≤25);y2=﹣![]() x2+5x﹣25(0≤x≤40);(2)当x=25时,y1 取得最大值,最大值为25m+142.当x=40时,y2有最大值,最大值为95.(3)应选择甲种货车,理由见解析.
x2+5x﹣25(0≤x≤40);(2)当x=25时,y1 取得最大值,最大值为25m+142.当x=40时,y2有最大值,最大值为95.(3)应选择甲种货车,理由见解析.
【解析】
(1)根据待定系数法即可求出两个函数解析式;(2)根据函数的性质和自变量的取值范围即可求解;(3)根据函数的最大值即可求得结果.
解:(1)根据题意,得
y1=(m+6)x﹣8,(0≤x≤25).
将x=10、y2=20,x=20、y2=55代入y2=ax2+bx﹣25,![]()
解得: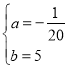
∴y2=![]() ,(0≤x≤40).
,(0≤x≤40).
(2)∵m是常数,(9≤m≤11),∴m+6>0,
∴y1 随x的增大而增大,
∴当x=25时,y1 取得最大值,最大值为25m+142.
∵y2=﹣![]() (x﹣50)2+100,
(x﹣50)2+100,
∴当x<50时,y随x的增大而增大,
∵0≤x≤40,
∴当x=40时,y2有最大值,最大值为95.
(3)∵y1 的最大值为25m+142.且9≤m≤11,
∴367≤y1≤417,
y2 有最大值为95,
∴95<367.
故应选择甲种货车.


科目:初中数学 来源: 题型:
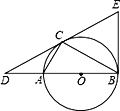
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0),与y轴交于点C.点D是抛物线上的一个动点,点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
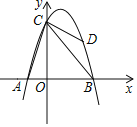
(1)求抛物线的解析式.
(2)当△BCD的面积等于△AOC的面积的![]() 时,求m的值.
时,求m的值.
(3)在抛物线的对称轴上是否存在一点Q,使得△QAC的周长最小,若存在,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=![]() x与反比例函数y=
x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4.
(k>0)的图象交于A、B两点,且点A的横坐标为4.

(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮用6张背面完全相同的纸牌进行摸牌游戏,游戏规则如下:将牌面分别标有数字1、3、6的三张纸牌给小明,将牌面分别标有数字2、4、5的三张纸牌给小亮,小明小亮分别将纸牌背面朝上,从各自的三张纸牌中随机抽出一张,并将抽出的两张卡片上的数字相加,如果和为偶数,则小明获胜;如果和为奇数,则小亮获胜.
(1)小明抽到标有数字6的纸牌的概率为 ;
(2)请用树状图或列表的方法求小亮获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com