
分析 将函数整理成关于x的一元二次方程,然后利用根的判别式列出不等式求解即可.
解答 解:∵y=$\frac{3{x}^{2}+x+2}{{x}^{2}+2x+1}$,
∴y(x2+2x+1)=3x2+x+2,
整理得,(y-3)x2+(2y-1)x+(y-2)=0,
∵关于x的一元二次方程有解,
∴△=b2-4ac=(2y-1)2-4(y-3)(y-2)≥0,
整理得,16y-24≥0,
解得y≤$\frac{3}{2}$,
所以,函数的最小值为$\frac{3}{2}$.
点评 本题考查了二次函数的最值,题目难度较大,将函数整理成关于x的一元二次方程并考虑利用根的判别式求解是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
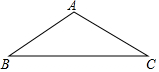 如图,某厂房人字架屋顶的上弦AB=AC=10米,∠β=α,则该屋顶的跨度BC为( )
如图,某厂房人字架屋顶的上弦AB=AC=10米,∠β=α,则该屋顶的跨度BC为( )| A. | 10sinα米 | B. | 10cosα米 | C. | 20sinα米 | D. | 20cosα米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
| 甲 | 3 | 4 | 4 | 3 | 4 | 5 | 5 | |
| 乙 | 4 | 3 | 3 | 4 | 3 | 5 | 6 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
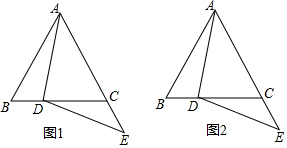 在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)
在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com